Диаграммы
Формальная арифметика
Рассмотрим множество натуральных чисел с операциями сложения и
умножения и его элементарную теорию 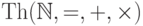 , то есть множество всех
истинных (в натуральном ряду) формул со сложением и умножением.
Это множество, очевидно, полно. Можно доказать
([5]), что оно неразрешимо (и, более
того, неарифметично, как говорит теорема Тарского).
, то есть множество всех
истинных (в натуральном ряду) формул со сложением и умножением.
Это множество, очевидно, полно. Можно доказать
([5]), что оно неразрешимо (и, более
того, неарифметично, как говорит теорема Тарского).
Отсюда следует, что теория 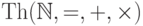 не
является конечно аксиоматизируемой. (В самом деле, эта теория
полна и неразрешима, и можно сослаться на
теорему 67.) Более того, это же рассуждение показывает, что не существует разрешимого
множества теорем этой теории, из которых бы выводились все
другие теоремы. Отсюда следует, что классическая система аксиом
формальной арифметики, называемая также арифметикой Пеано
(свойства арифметических операций плюс аксиомы индукции), не
может быть полной: существуют истинные формулы, невыводимые в
формальной арифметике. Это утверждение составляет содержание
знаменитой теоремы Геделя о неполноте.
не
является конечно аксиоматизируемой. (В самом деле, эта теория
полна и неразрешима, и можно сослаться на
теорему 67.) Более того, это же рассуждение показывает, что не существует разрешимого
множества теорем этой теории, из которых бы выводились все
другие теоремы. Отсюда следует, что классическая система аксиом
формальной арифметики, называемая также арифметикой Пеано
(свойства арифметических операций плюс аксиомы индукции), не
может быть полной: существуют истинные формулы, невыводимые в
формальной арифметике. Это утверждение составляет содержание
знаменитой теоремы Геделя о неполноте.
143. Покажите, что нельзя добавить к языку теории 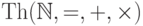 конечное число выразимых
предикатов так, чтобы после этого проходила элиминация
кванторов. (Указание: арифметическая иерархия не ограничивается
никаким конечным числом уровней.)
конечное число выразимых
предикатов так, чтобы после этого проходила элиминация
кванторов. (Указание: арифметическая иерархия не ограничивается
никаким конечным числом уровней.)
144. Покажите, что элементарная теория целых чисел со сложением и
умножением сводится к элементарной теории натуральных чисел со
сложением и умножением: по замкнутой формуле  со сложением
и умножением можно алгоритмически построить формулу
со сложением
и умножением можно алгоритмически построить формулу  с таким свойством:
с таким свойством:  истинна в
истинна в 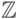 тогда и только тогда, когда
тогда и только тогда, когда  истинна в
истинна в  .
(Указание: целые числа можно кодировать парами натуральных.)
.
(Указание: целые числа можно кодировать парами натуральных.)
145. (Продолжение) Покажите, что верно и обратное: элементарная теория натуральных чисел сводится к элементарной теории целых чисел. (Указание. Если бы в целых числах был порядок, это было бы совсем просто. Чтобы его ввести, можно использовать теорему Лагранжа о том, что всякое натуральное число представимо в виде суммы четырех квадратов.)
Будет ли теория 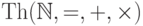 категоричной
в счетной мощности? Другими словами, имеет ли она
счетную модель, не изоморфную стандартной? Раньше,
для более простых ситуаций, нам удавалось указать такие модели
явно. Теперь это не удастся, но есть простое общее рассуждение,
устанавливающее существование нестандартной модели. (Оно
аналогично рассуждению, использованному при доказательстве
теоремы 52.)
категоричной
в счетной мощности? Другими словами, имеет ли она
счетную модель, не изоморфную стандартной? Раньше,
для более простых ситуаций, нам удавалось указать такие модели
явно. Теперь это не удастся, но есть простое общее рассуждение,
устанавливающее существование нестандартной модели. (Оно
аналогично рассуждению, использованному при доказательстве
теоремы 52.)
Рассмотрим последовательность формул 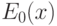 ,
, 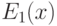 ,
, 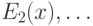 с единственным параметром
с единственным параметром  , где
, где 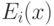 — любая формула, выражающая в стандартной модели свойство
— любая формула, выражающая в стандартной модели свойство 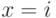 .
(Если бы у нас в языке была константа
.
(Если бы у нас в языке была константа  , можно было бы считать
, можно было бы считать 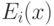 бескванторной формулой
бескванторной формулой 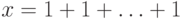 , в
правой части которой стоит терм с
, в
правой части которой стоит терм с  единицами.)
единицами.)
Добавим к сигнатуре новую константу  и рассмотрим теорию,
получаемую из
и рассмотрим теорию,
получаемую из 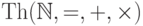 добавлением
счетного семейства формул
добавлением
счетного семейства формул 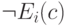 (по существу мы
добавляем формулы
(по существу мы
добавляем формулы 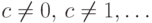 , записанные
подходящим образом). Любое конечное подмножество полученной
теории имеет модель (возьмем стандартный натуральный ряд и в
качестве
, записанные
подходящим образом). Любое конечное подмножество полученной
теории имеет модель (возьмем стандартный натуральный ряд и в
качестве  выберем достаточно большое число). Следовательно
(теорема 50 о компактности), и вся эта теория совместна. Рассмотрим ее счетную нормальную
модель и забудем о символе
выберем достаточно большое число). Следовательно
(теорема 50 о компактности), и вся эта теория совместна. Рассмотрим ее счетную нормальную
модель и забудем о символе  ; получится некоторая
интерпретация сигнатуры
; получится некоторая
интерпретация сигнатуры 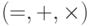 . Она будет
элементарно эквивалентна стандартному натуральному ряду (все
истинные в
. Она будет
элементарно эквивалентна стандартному натуральному ряду (все
истинные в  формулы будут истинны по построению, а
все ложные будут ложны, так как их отрицания истинны).
формулы будут истинны по построению, а
все ложные будут ложны, так как их отрицания истинны).
Осталось показать, что она не будет изоморфной натуральному
ряду. В самом деле, рассмотрим элемент, который является
значением константы  в нестандартной модели. Он не может
переходить ни в какое натуральное число
в нестандартной модели. Он не может
переходить ни в какое натуральное число  , поскольку для
соответствующих (друг другу при изоморфизме) элементов выполнены
одни и те же формулы,
, поскольку для
соответствующих (друг другу при изоморфизме) элементов выполнены
одни и те же формулы, 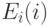 истинно в натуральном ряду и
истинно в натуральном ряду и 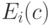 ложно в новой интерпретации.
ложно в новой интерпретации.
146. Покажите, что найдется нормальная интерпретация сколь угодно большой мощности, элементарно эквивалентная натуральным числам со сложением и умножением.
