Исчисление предикатов
Общезначимые формулы
Исчисление высказываний ( "Исчисление высказываний" ) позволяло выводить все тавтологии из некоторого набора базисных тавтологий (названных аксиомами) с помощью некоторых правил вывода (на самом деле единственного правила modus ponens). Сейчас мы хотим решить аналогичную задачу для формул первого порядка. Соответствующее исчисление называется исчислением предикатов.
Пусть фиксирована некоторая сигнатура  .
Формула
.
Формула  этой сигнатуры (возможно, с параметрами)
называется общезначимой, если она
истинна в любой интерпретации сигнатуры
этой сигнатуры (возможно, с параметрами)
называется общезначимой, если она
истинна в любой интерпретации сигнатуры  на любой
оценке.
на любой
оценке.
Общезначимые формулы в логике предикатов играют ту же роль, что
тавтологии в логике высказываний. Между ними есть и формальная
связь: если взять любую тавтологию и вместо входящих в нее
пропозициональных переменных подставить произвольные формулы
сигнатуры  , получится общезначимая формула. В самом
деле, пусть есть некоторая интерпретация сигнатуры
, получится общезначимая формула. В самом
деле, пусть есть некоторая интерпретация сигнатуры  и
некоторая оценка (то есть фиксированы значения индивидных
переменных). Тогда каждая из подставленных формул станет
истинной или ложной, а значение всей формулы определяется с
помощью таблиц истинности для логических связок, то есть по тем
же правилам, что в логике высказываний.
и
некоторая оценка (то есть фиксированы значения индивидных
переменных). Тогда каждая из подставленных формул станет
истинной или ложной, а значение всей формулы определяется с
помощью таблиц истинности для логических связок, то есть по тем
же правилам, что в логике высказываний.
Конечно, бывают и другие общезначимые формулы, не являющиеся частным случаями пропозициональных тавтологий. Например, формула

 — произвольная формула):
— произвольная формула):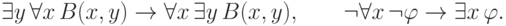
87. Будет ли общезначима формула
(а)  ; (б)
; (б)  ?
?
Многие вопросы можно сформулировать как вопросы об
общезначимости некоторых формул. Например, можно записать
свойства рефлексивности, транзитивности и антисимметричности в
виде формул  ,
,  и
и  сигнатуры
сигнатуры 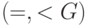 и затем написать формулу
и затем написать формулу
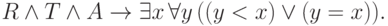
88. Напишите формулы 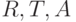 и проверьте, что приведенная нами
формула не общезначима, хотя истинна во всех конечных интерпретациях.
и проверьте, что приведенная нами
формула не общезначима, хотя истинна во всех конечных интерпретациях.
89. Известно, что формула истинна во всех конечных и счетных интерпретациях. Можно ли из этого заключить, что она общезначима? (Указание: воспользуйтесь теоремой Левенгейма-Сколема об элементарной подмодели.)
Две формулы  и
и  (с параметрами или без)
называются эквивалентными, если в любой интерпретации и
на любой оценке, на которой истинна одна из них, истинна и
другая. Это определение равносильно такому: формула
(с параметрами или без)
называются эквивалентными, если в любой интерпретации и
на любой оценке, на которой истинна одна из них, истинна и
другая. Это определение равносильно такому: формула  общезначима. Здесь, напомним,
общезначима. Здесь, напомним,  есть сокращение для
есть сокращение для 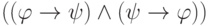 .
.
Общезначимость любой формулы  очевидно равносильна
общезначимости ее замыкания — формулы, которая получится,
если слева к
очевидно равносильна
общезначимости ее замыкания — формулы, которая получится,
если слева к  приписать кванторы всеобщности по всем
параметрам.
приписать кванторы всеобщности по всем
параметрам.
Двойственное к общезначимости понятие — выполнимость. Формула
называется выполнимой, если она истинна в некоторой
интерпретации на некоторой оценке. Очевидно, формула  общезначима тогда и только тогда, когда формула
общезначима тогда и только тогда, когда формула 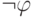 не является выполнимой.
не является выполнимой.
90. Закончите утверждение: выполнимость формулы с параметрами равносильна выполнимости
замкнутой формулы, которая получится, если\, 
Чтобы проверить, является ли формула тавтологией, достаточно подставить в нее все возможные наборы значений переменных. Хотя этот процесс может быть на практике невыполним (наборов слишком много), теоретически мы имеем простой алгоритм проверки, является ли формула тавтологией. Для общезначимых формул в общем случае такого алгоритма не существует (теорема Черча; ее доказательство можно прочесть в [5]); он есть только для очень ограниченных классов формул. Например, если сигнатура содержит только нульместные предикатные символы, то задача по существу сводится к проверке тавтологичности (в этом случае кванторы фиктивны). Чуть более сложен случай с одноместными предикатами.
91. Пусть сигнатура  содержит только одноместные предикаты.
Докажите, что всякая выполнимая формула этой сигнатуры,
содержащая
содержит только одноместные предикаты.
Докажите, что всякая выполнимая формула этой сигнатуры,
содержащая  различных предикатов, выполнима в некоторой
конечной интерпретации, содержащей не более
различных предикатов, выполнима в некоторой
конечной интерпретации, содержащей не более  элементов. Как
использовать этот факт для алгоритмической проверки выполнимости
формул такой сигнатуры?
элементов. Как
использовать этот факт для алгоритмической проверки выполнимости
формул такой сигнатуры?
