Исчисление предикатов
Корректность исчисления предикатов
Теорема 43. Всякая выводимая в исчислении предикатов формула является общезначимой.
Для исчисления высказываний проверка корректности была тривиальной — надо было по таблице проверить, что все аксиомы (1)-(11) являются тавтологиями. С этими аксиомами и сейчас нет проблем. Но в двух следующих аксиомах есть ограничение на корректность подстановки, без которого они могут не быть общезначимыми. Естественно, это ограничение должно быть использовано и в доказательстве корректности, и это потребует довольно скучных рассуждений — тем более скучных, что сам факт кажется ясным и так. Тем не менее такие рассуждения надо уметь проводить, так что мы ничего пропускать не будем.
Итак, пусть фиксирована сигнатура  , а также некоторая
интерпретация этой сигнатуры. Всюду далее, говоря о термах и
формулах, мы имеем в виду термы и формулы этой сигнатуры, а
говоря об их значениях, имеем в виду значения в этой интерпретации.
, а также некоторая
интерпретация этой сигнатуры. Всюду далее, говоря о термах и
формулах, мы имеем в виду термы и формулы этой сигнатуры, а
говоря об их значениях, имеем в виду значения в этой интерпретации.
Лемма 1. Пусть  и
и  — термы, а
— термы, а  — переменная. Тогда
— переменная. Тогда
 = [u](\pi + (\xi\mapsto [t](\pi)))](/sites/default/files/tex_cache/f5f49409a5e22f9da4686efcf9422d82.png)
 .
.Напомним обозначения: в левой части мы подставляем  вместо
вместо  в терм
в терм  , и берем значение получившегося терма на оценке
, и берем значение получившегося терма на оценке  . В правой части стоит значение терма
. В правой части стоит значение терма  на оценке, которая
получится из
на оценке, которая
получится из  , если значение переменной
, если значение переменной  изменить и
считать равным значению терма
изменить и
считать равным значению терма  на оценке
на оценке  .
.
В сущности, это утверждение совершенно тривиально: оно говорит,
например, что значение  при
при 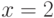 равно
значению
равно
значению 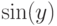 при
при 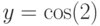 . Но раз уж мы взялись все
доказывать формально, докажем его индукцией по построению терма
. Но раз уж мы взялись все
доказывать формально, докажем его индукцией по построению терма  . Если
терм
. Если
терм  есть переменная, отличная от
есть переменная, отличная от  , то ни
подстановка, ни изменение оценки не сказываются на значении терма
, то ни
подстановка, ни изменение оценки не сказываются на значении терма  . Для
случая
. Для
случая  получаем
получаем ](/sites/default/files/tex_cache/e491a156c737bb0414d0327beb007fa6.png) слева и справа. Если
терм получается из других термов применением функционального символа,
то подстановка выполняется отдельно в каждом из этих термов, так
что искомое равенство также сохраняется. Лемма 1 доказана.
слева и справа. Если
терм получается из других термов применением функционального символа,
то подстановка выполняется отдельно в каждом из этих термов, так
что искомое равенство также сохраняется. Лемма 1 доказана.
Аналогичное утверждение для формул таково:
Лемма 2. Пусть  — формула,
— формула,  —
терм, а
—
терм, а  — переменная, причем подстановка
— переменная, причем подстановка  вместо
вместо  в формулу
в формулу  корректна. Тогда
корректна. Тогда
 = [\varphi](\pi + (\xi\mapsto [t](\pi)))](/sites/default/files/tex_cache/82d7ad7bc4521d202ada518943f5aa3e.png)
 .
.Поясним смысл этой леммы на примере. Пусть  является
единственным параметром формулы
является
единственным параметром формулы  , а
, а  —
константа. Тогда формула
—
константа. Тогда формула 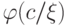 замкнута; лемма утверждает, что
ее истинность равносильна истинности
замкнута; лемма утверждает, что
ее истинность равносильна истинности  на оценке, при
которой значение переменной
на оценке, при
которой значение переменной  есть элемент интерпретации,
соответствующий константе
есть элемент интерпретации,
соответствующий константе  .
.
Доказательство леммы проведем индукцией по построению
формулы  . Для атомарных формул это утверждение является
прямым следствием леммы 1. Кроме того, из определения
истинностного значения формулы и из определения подстановки
ясно, что если утверждение леммы 2 верно для двух формул
. Для атомарных формул это утверждение является
прямым следствием леммы 1. Кроме того, из определения
истинностного значения формулы и из определения подстановки
ясно, что если утверждение леммы 2 верно для двух формул 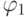 и
и 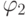 , то оно верно для их любой их
логической комбинации (конъюнкции, дизъюнкции и импликации);
аналогично для отрицания.
, то оно верно для их любой их
логической комбинации (конъюнкции, дизъюнкции и импликации);
аналогично для отрицания.
Единственный нетривиальный случай — формула, начинающаяся с
квантора. Здесь наши определения вступают в игру.
Пусть  имеет вид
имеет вид 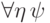 . Есть два
принципиально разных случая: либо
. Есть два
принципиально разных случая: либо  является параметром
формулы
является параметром
формулы  (т. е. формулы
(т. е. формулы 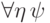 ), либо нет. Во втором случае
), либо нет. Во втором случае 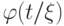 совпадает с
совпадает с  , а изменение
значения переменной
, а изменение
значения переменной  в оценке
в оценке  не влияет на значение
формулы
не влияет на значение
формулы  , так что все сходится. Осталось разобрать случай, когда
, так что все сходится. Осталось разобрать случай, когда  является параметром формулы
является параметром формулы 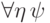 (отсюда следует, что
(отсюда следует, что  не совпадает с
не совпадает с  ). По определению
корректной подстановки, в этом случае переменная
). По определению
корректной подстановки, в этом случае переменная  не
входит в терм
не
входит в терм  и подстановка
и подстановка 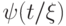 корректна.
Тогда
корректна.
Тогда
=
[\forall \eta\, (\psi(t/\xi))](\pi) =\\
&=\wedge_m [\psi(t/\xi)](\pi+(\eta\mapsto m)) = \\
&=\wedge_m [\psi](\pi+(\eta\mapsto m)+
(\xi\mapsto[t](\pi+(\eta\mapsto m)))).
\end{align*}](/sites/default/files/tex_cache/8edc55159ca849c82ad22a726d5a832e.png)
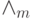 означает конъюнкцию по всем элементам из носителя
интерпретации) и предположением индукции для формулы
означает конъюнкцию по всем элементам из носителя
интерпретации) и предположением индукции для формулы  .
Теперь надо заметить, что переменная
.
Теперь надо заметить, что переменная  не входит в
не входит в  по предположению корректности, и потому значение терма
по предположению корректности, и потому значение терма  не
изменится, если заменить
не
изменится, если заменить  на
на  . Далее,
. Далее,  и
и  различны, поэтому два изменения в
различны, поэтому два изменения в  можно переставить местами.
Используя эти соображения, можно продолжить цепочку равенств:
можно переставить местами.
Используя эти соображения, можно продолжить цепочку равенств:)+(\eta\mapsto m)) = \\
&=[\forall \eta\,\psi](\pi+(\xi\mapsto [t](\pi))) = \\
&=[\varphi](\pi+(\xi\mapsto [t](\pi))),
\end{align*}](/sites/default/files/tex_cache/9a1311967ef03c9c1a126333cf98d0a1.png)
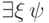 разбирается аналогично, надо только
разбирается аналогично, надо только 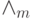 заменить на
заменить на 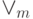 . Лемма 2 доказана.
. Лемма 2 доказана.Теперь уже ясно, почему формула

 (если подстановка
корректна). В самом деле, если левая часть импликации истинна
на
(если подстановка
корректна). В самом деле, если левая часть импликации истинна
на  , то
, то  будет истинна на любой оценке
будет истинна на любой оценке 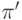 , которая отличается от
, которая отличается от  лишь значением переменной
лишь значением переменной  . В частности,
. В частности,  будет истинна и на оценке
будет истинна и на оценке )](/sites/default/files/tex_cache/48a6ae5554454c820ead4fd1cce33fa7.png) , что по только что доказанной лемме 2 означает, что
правая часть импликации истинна на
, что по только что доказанной лемме 2 означает, что
правая часть импликации истинна на  .
.Общезначимость формулы
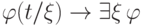
Нам осталось проверить, что правила вывода сохраняют общезначимость. Для правила MP это очевидно (как и в случае исчисления высказываний). Проверим это для правил Бернайса. Это совсем несложно, так как здесь нет речи ни о каких корректных подстановках.
Пусть, например, формула  общезначима и
переменная
общезначима и
переменная  не является параметром формулы
не является параметром формулы  .
Проверим, что формула
.
Проверим, что формула 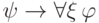 общезначима,
то есть истинна на любой оценке
общезначима,
то есть истинна на любой оценке  (в любой интерпретации). В
самом деле, пусть
(в любой интерпретации). В
самом деле, пусть  истинна на оценке
истинна на оценке  . Тогда
она истинна и на любой оценке
. Тогда
она истинна и на любой оценке 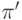 , отличающейся от
, отличающейся от  только значением переменной
только значением переменной  (значение переменной
(значение переменной  не
влияет на истинность
не
влияет на истинность  , так как
, так как  не является
параметром). Значит, и формула
не является
параметром). Значит, и формула  истинна на любой такой
оценке
истинна на любой такой
оценке 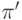 . А это в точности означает, что
. А это в точности означает, что 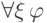 истинна на оценке
истинна на оценке  , что и требовалось.
, что и требовалось.
Для второго правила Бернайса рассуждение симметрично.
Пусть формула  общезначима и
переменная
общезначима и
переменная  не является параметром формулы
не является параметром формулы  .
Покажем, что формула
.
Покажем, что формула 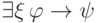 общезначима. В самом
деле, пусть ее левая часть истинна на некоторой оценке
общезначима. В самом
деле, пусть ее левая часть истинна на некоторой оценке  . По
определению истинности формулы, начинающейся с квантора
существования, это означает, что найдется оценка
. По
определению истинности формулы, начинающейся с квантора
существования, это означает, что найдется оценка 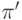 , которая
отличается от
, которая
отличается от  только на переменной
только на переменной  , для
которой
, для
которой ](/sites/default/files/tex_cache/9b377a2086ed4f639b83fa09e2f69ff7.png) истинно. Тогда и
истинно. Тогда и ](/sites/default/files/tex_cache/7130db3bc3e7d28a5133a69dcb97e3a6.png) истинно. Но переменная
истинно. Но переменная  не является параметром формулы
не является параметром формулы  ,
так что
,
так что =[\psi](\pi)](/sites/default/files/tex_cache/ea6326a0e442dbae7173d8ef074879e9.png) . Следовательно, формула
. Следовательно, формула  истинна на оценке
истинна на оценке  , что и требовалось доказать.
, что и требовалось доказать.
