Полнота исчисления предикатов
Выводы в исчислении предикатов
Примеры выводимых формул
Прежде чем доказывать теорему Геделя о полноте исчисления предикатов, мы должны приобрести некоторый опыт построения выводов в этом исчислении.
- Прежде всего отметим, что возможность сослаться на
теорему о полноте исчисления высказываний и считать выводимым любой
частный случай пропозициональной тавтологии сильно облегчает
жизнь. Например, пусть мы вывели две формулы
 и
и  и хотим теперь вывести формулу
и хотим теперь вывести формулу 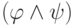 . Это просто:
заметим, что формула
. Это просто:
заметим, что формула  является частным случаем пропозициональной тавтологии (а на
самом деле и аксиомой) и дважды применяем правило MP.
является частным случаем пропозициональной тавтологии (а на
самом деле и аксиомой) и дважды применяем правило MP. - Другой пример такого же рода: если формула
 выводима, то выводима и формула
выводима, то выводима и формула  , поскольку
импликацияявляется частным случаем пропозициональной тавтологии.
, поскольку
импликацияявляется частным случаем пропозициональной тавтологии.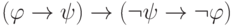
- Еще один пример: если выводимы формулы
 и
и  , то выводима и формула
, то выводима и формула  , поскольку формулаявляется частным случаем пропозициональной тавтологии.
, поскольку формулаявляется частным случаем пропозициональной тавтологии.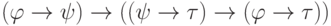
- Для произвольной формулы
 выведем формулуВ самом деле, подстановка переменной вместо себя всегда допустима, поэтому формулы
выведем формулуВ самом деле, подстановка переменной вместо себя всегда допустима, поэтому формулы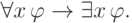
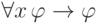 и
и 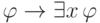 являются
аксиомами. Остается воспользоваться предыдущим замечанием.
являются
аксиомами. Остается воспользоваться предыдущим замечанием. - Для произвольной формулы
 выведем формулуФормулы
выведем формулуФормулы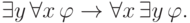
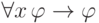 и
и 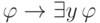 являются аксиомами. С их помощью выводим
формулу
являются аксиомами. С их помощью выводим
формулу  . Теперь заметим, что левая часть импликации не имеет
параметра
. Теперь заметим, что левая часть импликации не имеет
параметра  , а правая часть не имеет параметра
, а правая часть не имеет параметра  ,
так что можно применить два правила Бернайса (в любом порядке) и
добавить справа квантор
,
так что можно применить два правила Бернайса (в любом порядке) и
добавить справа квантор 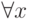 , а слева — квантор
, а слева — квантор  .
. - Предположим, что формула
 выводима, а
выводима, а  — произвольная переменная. Покажем, что в этом случае выводима
формула
— произвольная переменная. Покажем, что в этом случае выводима
формула 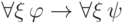 . В самом
деле, формула
. В самом
деле, формула  является
аксиомой. Далее выводим (с помощью пропозициональных тавтологий
и правила MP) формулу
является
аксиомой. Далее выводим (с помощью пропозициональных тавтологий
и правила MP) формулу 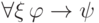 ; остается
воспользоваться правилом Бернайса (левая часть не имеет параметра
; остается
воспользоваться правилом Бернайса (левая часть не имеет параметра  ).
). - Аналогичным образом из выводимости формулы
 следует выводимость формулы
следует выводимость формулы 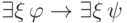 ,
только надо начать с аксиомы
,
только надо начать с аксиомы 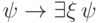 , затем
получить
, затем
получить 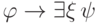 , а потом применить
правило Бернайса.
, а потом применить
правило Бернайса. -
Таким образом, если формулы
 и
и  доказуемо
эквивалентны (это значит, что импликации
доказуемо
эквивалентны (это значит, что импликации  и
и  выводимы), то формулы
выводимы), то формулы 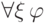 и
и 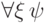 также доказуемо эквивалентны. (Аналогичное
утверждение верно и для формул
также доказуемо эквивалентны. (Аналогичное
утверждение верно и для формул 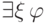 и
и 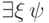 .)
.)Теперь несложно доказать и более общий факт: замена подформулы на доказуемо эквивалентную дает доказуемо эквивалентную формулу.
- Выведем формулу
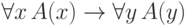 (здесь
(здесь  — одноместный предикатный символ). Это несложно: начнем с
аксиомы
— одноместный предикатный символ). Это несложно: начнем с
аксиомы  , в ней левая часть не имеет
параметра
, в ней левая часть не имеет
параметра  и потому по правилу Бернайса из нее получается
искомая формула. Этот пример показывает, что связанные
переменные можно переименовывать, не меняя смысла формулы
и потому по правилу Бернайса из нее получается
искомая формула. Этот пример показывает, что связанные
переменные можно переименовывать, не меняя смысла формулы -
Выведем формулы, связывающие кванторы всеобщности и существования:
Напомним, что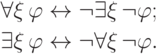
 мы считаем
сокращением для
мы считаем
сокращением для  ,
так что нам надо вывести четыре формулы.
,
так что нам надо вывести четыре формулы.
Начнем с формулы
 . Имея в виду правило Бернайса,
достаточно вывести формулу
. Имея в виду правило Бернайса,
достаточно вывести формулу  . Тавтология
. Тавтология  позволяет вместо этого выводить
формулу
позволяет вместо этого выводить
формулу 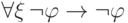 , которая
является аксиомой.
, которая
является аксиомой.В только что выведенной формуле
 можно в
качестве
можно в
качестве  взять любую формулу, в том числе начинающуюся
с отрицания. Подставив
взять любую формулу, в том числе начинающуюся
с отрицания. Подставив 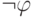 вместо
вместо  ,
получимгде
,
получимгде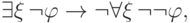
 доказуемо эквивалентна
доказуемо эквивалентна  и потому может быть заменена на
и потому может быть заменена на  . После этого правило
контрапозиции (если из
. После этого правило
контрапозиции (если из  следует
следует 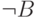 , то
из
, то
из  следует
следует 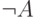 ) дает
) дает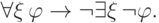
Выведем третью формулу:
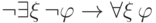 . По
правилу Бернайса достаточно вывести
. По
правилу Бернайса достаточно вывести  , что после
контрапозиции превращается в аксиому
, что после
контрапозиции превращается в аксиому 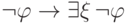 .
.Четвертая формула получится, если заменить в третьей
 на
на  и применить контрапозицию.
и применить контрапозицию.
