НОУ ИНТУИТ | Языки и исчисления. Лекция 10: Полнота исчисления предикатов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 24.04.2007 | Доступ: свободный | Студентов: 722 / 35 | Оценка: 4.60 / 4.30 | Длительность: 25:56:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Выводимость из посылок

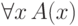В исчислении высказываний важную роль играло понятие выводимости из посылок и связанная с ним лемма о дедукции. Для исчисления предикатов ситуация немного меняется. Если разрешить использовать посылки наравне с аксиомами безо всяких ограничений, то утверждение, аналогичное лемме о дедукции, будет неверным. Например, из формулы A(x) можно вывести формулу $\forall x\, A(x)$ (как мы видели при обсуждении правила обобщения). Но импликация 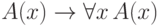$A(x)\to\forall x\,A(x)$ не является выводимой (поскольку не общезначима).

Поэтому мы ограничимся случаем, когда все посылки являются замкнутыми формулами. Пусть $\Gamma$ — произвольное множество замкнутых формул рассматриваемой нами сигнатуры $\sigma$ . (Такие множества называют теориями в сигнатуре $\sigma$ .) Говорят, что формула выводима из $\Gamma$ , если ее можно вывести, используя наравне с аксиомами формулы из $\Gamma$ . 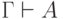Как и для исчисления высказываний, мы пишем $\Gamma\vdash A$ . Выводимые из $\Gamma$ формулы называют также теоремами теории $\Gamma$ .

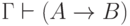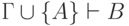Лемма о дедукции для исчисления предикатов. Пусть $\Gamma$ — множество замкнутых формул, а — замкнутая формула. Тогда $\Gamma \vdash (A\to B)$ тогда и только тогда, когда $\Gamma\cup\{A\} \vdash B$ .

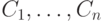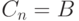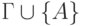Доказательство проходит по той же схеме, что и для исчисления высказываний : к формулам $C_1,\dots,C_n$ , образующим вывод C_n=B из $\Gamma\cup\{A\}$ , мы приписываем посылку и дополняем полученную последовательность

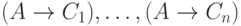
$(A\to C_1),\dots,(A\to C_n)$

до вывода из $\Gamma$ . Отличие от пропозиционального случая в том, что в выводе могут встречаться правила Бернайса. Например, от выводимости формулы

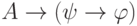
$A\to(\psi\to\varphi)$

надо перейти к выводимости формулы

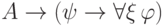
$A\to(\psi\to\forall\xi\,\varphi)$

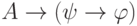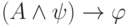(в которой переменная $\xi$ не является параметром формулы $\psi$ ). Это несложно сделать, если заметить, что в силу пропозициональных тавтологий можно перейти от $A\to(\psi\to\varphi)$ к $(A\land\psi)\to\varphi$ , затем применить правило Бернайса (это законно, так как переменная $\xi$ не является параметром формулы $\psi$ , а формула

замкнута по предположению). Получится выводимая из $\Gamma$ формула

$(A\land\psi)\to\forall\xi\,\varphi,$

и остается вернуть

из конъюнкции в посылку.

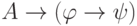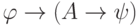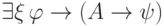Сходным образом рассматривается и второе правило Бернайса. Если выводима формула $A\to(\varphi\to\psi)$ , то в силу пропозициональных тавтологий выводима формула $\varphi\to(A\to\psi)$ , к которой можно применить правило Бернайса и получить $\exists\xi\,\varphi\to(A\to\psi)$ , после чего вернуть назад с помощью пропозициональной тавтологии. Лемма о дедукции доказана.

Отметим теперь несколько полезных свойств выводимости из посылок.

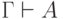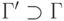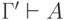Если $\Gamma\vdash A$ и $\Gamma' \supset \Gamma$ , то $\Gamma' \vdash A$ . (Очевидно следует из определения.)
Если 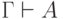$\Gamma\vdash A$ , то существует конечное множество 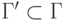$\Gamma' \subset \Gamma$ , для которого 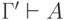$\Gamma' \vdash A$ . (Вывод конечен и потому может использовать лишь конечное число формул.)
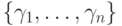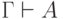Если $\Gamma$ конечно и равно $\{\gamma_1,\dots,\gamma_n\}$ , то $\Gamma\vdash A$ равносильно выводимости (без посылок) формулы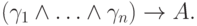
$(\gamma_1\land\ldots\land\gamma_n)\to A.$

В самом деле, если 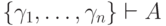$\{\gamma_1,\dots,\gamma_n\}\vdash A$ , то многократное применение леммы о дедукции дает
$\vdash \gamma_1\to(\gamma_2\to(\ldots(\gamma_n\to A)\ldots)),$
и остается воспользоваться надлежащей пропозиональной тавтологией. (В обратную сторону рассуждение также проходит без труда.)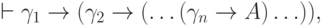
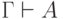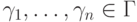Комбинируя три предыдущих замечания, приходим к такому эквивалентному определению выводимости из посылок: $\Gamma\vdash A$ , если найдутся формулы $\gamma_1,\dots,\gamma_n\in \Gamma$ , для которых
$\vdash \gamma_1\to(\gamma_2\to(\ldots(\gamma_n\to A)\ldots)).$
Это определение имеет смысл и для формул с параметрами, так что если уж определять выводимость из посылок с параметрами (чего обычно избегают), то именно так.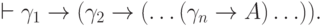

Понятие выводимости из посылок позволяет переформулировать теорему о корректности исчисления предикатов.

Говорят, что интерпретация сигнатуры $\sigma$ является моделью теории $\Gamma$ , если все формулы из $\Gamma$ истинны в .

Теорема 44 (о корректности; переформулировка). Все теоремы теории $\Gamma$ истинны в любой модели теории $\Gamma$ .

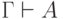Если формула является теоремой теории $\Gamma$ (т. е. $\Gamma\vdash A$ ), найдутся формулы 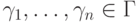$\gamma_1,\dots,\gamma_n\in\Gamma$ , для которых

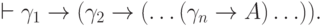
$\vdash \gamma_1\to(\gamma_2\to(\ldots(\gamma_n\to A)\ldots)).$

По теореме о корректности (в уже известной нам форме) эта формула будет истинна во всех интерпретациях, в частности в

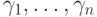. Поскольку $\gamma_1,\dots,\gamma_n$ истинны в

, то и формула

истинна в

(на любой оценке).

В следующих задачах — и только в них — знак 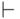$\vdash$ понимается в описанном выше смысле (в посылках допускаются параметры).

95. Пусть $\Gamma$ — множество произвольных (не обязательно замкнутых) формул. (а) Пусть существует "вывод" некоторой формулы $\varphi$ , в котором наравне с аксиомами используются формулы из $\Gamma$ , при этом все применения правил Бернайса предшествуют появлению формул из $\Gamma$ . Покажите, что $\Gamma\vdash\varphi$ . Покажите, что верно и обратное утверждение. (б) Покажите, если в "выводе" формулы $\varphi$ наравне с аксиомами используются формулы из $\Gamma$ , но правила Бернайса не применяются по переменным, свободным в $\Gamma$ , то ${\Gamma\vdash\varphi}$ .

96. Покажите, что правила Бернайса можно переписать так:

$\frac{\Gamma, A\vdash B\mathstrut} {\Gamma, A \vdash \forall\xi\,B\mathstrut} \qquad \frac{\Gamma, B\vdash A\mathstrut} {\Gamma, \exists\xi\,\vdash A\mathstrut},$

где переменная $\xi$ не является параметром формулы

, а также параметром формул из $\Gamma$ . (В первом правиле мы для симметрии выделили формулу

, хотя она ничем не отличается от формул из $\Gamma$ .)

Дальше >>

Авторизоваться

Языки и исчисления

Полнота исчисления предикатов

Выводимость из посылок

Вопросы и ответы