Исчисление высказываний
Напомним, что тавтологией мы называли пропозициональную формулу, истинную при всех значениях переменных. Оказывается, что все тавтологии можно получить из некоторого набора "аксиом" с помощью "правил вывода", которые имеют чисто синтаксический характер и никак не апеллируют к смыслу формулы, ее истинности и т. д. Эту задачу решает так называемое исчисление высказываний. В этой лекции мы перечислим аксиомы и правила вывода этого исчисления, и приведем несколько доказательств теоремы о полноте (которая утверждает, что всякая тавтология выводима в исчислении высказываний).
Исчисление высказываний (ИВ)
Каковы бы ни были формулы 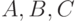 , следующие формулы называют
аксиомами исчисления высказываний:
, следующие формулы называют
аксиомами исчисления высказываний:
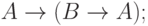 |
( 1) |
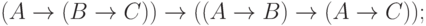 |
( 2) |
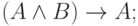 |
( 3) |
 |
( 4) |
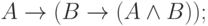 |
( 5) |
 |
( 6) |
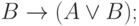 |
( 7) |
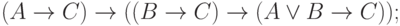 |
( 8) |
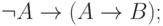 |
( 9) |
 |
( 10) |
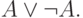 |
( 11) |
Как говорят, мы имеем здесь одиннадцать "схем аксиом"; из каждой схемы можно получить различные конкретные аксиомы, заменяя входящие в нее буквы на пропозициональные формулы.
Единственным правилом вывода исчисления высказываний является
правило со средневековым названием "modus ponens" (MP).
Это правило разрешает получить (вывести) из формул  и
и  формулу
формулу  .
.
Выводом в исчислении высказываний называется конечная последовательность формул, каждая из которых есть аксиома или получается из предыдущих по правилу modus ponens.
Вот пример вывода (в нем первая формула является частным случаем схемы (1), вторая — схемы (2), а последняя получается из двух предыдущих по правилу modus ponens):
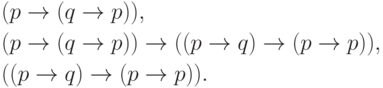
Пропозициональная формула  называется выводимой
в исчислении высказываний, или теоремой исчисления
высказываний, если существует вывод, в котором последняя формула
равна
называется выводимой
в исчислении высказываний, или теоремой исчисления
высказываний, если существует вывод, в котором последняя формула
равна  . Такой вывод называют выводом формулы
. Такой вывод называют выводом формулы  . (В
принципе можно было бы и не требовать, чтобы формула
. (В
принципе можно было бы и не требовать, чтобы формула  была последней —
все дальнейшие формулы можно просто вычеркнуть.)
была последней —
все дальнейшие формулы можно просто вычеркнуть.)
Как мы уже говорили, в исчислении высказываний выводятся все тавтологии и только они. Обычно это утверждение разбивают на две части: простую и сложную. Начнем с простой:
Теорема 17 (О корректности ИВ). Всякая теорема исчисления высказываний есть тавтология.
Несложно проверить, что все аксиомы — тавтологии. Для примера проделаем это для самой длинной аксиомы (точнее, схемы аксиом) — для второй. В каком случае формула

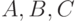 — некоторые формулы) могла бы быть ложной? Для
этого посылка
— некоторые формулы) могла бы быть ложной? Для
этого посылка 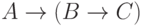 должна быть истинной, а заключение
должна быть истинной, а заключение  — ложным. Чтобы заключение было ложным,
формула
— ложным. Чтобы заключение было ложным,
формула 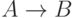 должна быть истинной, а формула
должна быть истинной, а формула  —
ложной. Последнее означает, что
—
ложной. Последнее означает, что  истинна, а
истинна, а  ложна. Таким образом, мы знаем, что
ложна. Таким образом, мы знаем, что  ,
,  и
и 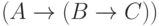 истинны. Отсюда следует, что
истинны. Отсюда следует, что  и
и  истинны,
и потому
истинны,
и потому  истинна — противоречие. Значит, наша формула не бывает ложной.
истинна — противоречие. Значит, наша формула не бывает ложной.Корректность правила MP также очевидна: если формулы  и
и  всегда истинны, то по определению импликации
формула
всегда истинны, то по определению импликации
формула  также всегда истинна. Таким образом, все формулы, входящие в
выводы (все теоремы) являются тавтологиями.
также всегда истинна. Таким образом, все формулы, входящие в
выводы (все теоремы) являются тавтологиями.
Гораздо сложнее доказать обратное утверждение.
