Исчисление высказываний

Второе доказательство теоремы о полноте

Это доказательство, в отличие от предыдущего, обобщается на более сложные случаи (исчисление предикатов, интуиционистское исчисление высказываний).

Начнем с такого определения: множество формул называется совместным,если существует набор значений переменных, при которых все формулы из истинны. Заметим, что формула является тавтологией тогда и только тогда, когда множество, состоящее из единственной формулы , не является совместным. 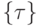Для случая одной формулы есть специальный термин: формула выполнима, если существуют значения переменных, при которых она истинна, то есть если множество совместно. Тавтологии — это формулы, отрицания которых не выполнимы.

Множество формул называется противоречивым, если из него одновременно выводятся формулы и 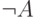. Мы знаем, что в этом случае из него выводятся вообще все формулы. (В противном случае называется непротиворечивым.)

Теорема 19 (корректность исчисления высказываний, вторая форма). Всякое совместное множество формул непротиворечиво.

В самом деле, пусть совместное множество противоречиво. Так как оно совместно, существуют значения переменных, при которых все формулы из истинны. С другой стороны, из выводится некоторая формула и ее отрицание. Может ли так быть?

Оказывается, что нет. Мы уже видели, что всякая выводимая формула истинна при всех значениях переменных (является тавтологией). Справедливо и несколько более общее утверждение: если 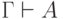и при некоторых значениях переменных все формулы из истинны, то и формула истинна при этих значениях переменных. (Как и раньше, это легко доказывается индукцией по построению вывода из .)

В нашей ситуации это приводит к тому, что на выполняющем наборе значений переменных для должны быть истинны обе формулы и 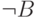, что, разумеется, невозможно.

Мы называем это утверждение другой формой теоремы о корректности исчисления высказываний, поскольку из него формально можно вывести, что всякая теорема является тавтологией: если — теорема, то множество противоречиво (из него выводятся и 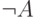), потому несовместно, значит, 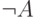всегда ложна, поэтому всегда истинна.

Теорема 20 (полнота исчисления высказываний, вторая форма). Всякое непротиворечивое множество совместно.

Нам дано непротиворечивое множество , а надо найти такие значения переменных, при которых все формулы из истинны. (Вообще говоря, множество может быть бесконечно и содержать бесконечное число разных переменных.)

Пусть есть какая-то переменная , встречающаяся в формулах из семейства . Нам надо решить, сделать ли ее истинной или ложной. Если оказалось так, что из выводится формула , то выбора нет: она обязана быть истинной в тех наборах, где формулы из истинны (как мы видели при доказательстве корректности). По тем же причинам, если из выводится 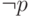, то в выполняющем наборе переменная обязательно будет ложной.

Если оказалось так, что для любой переменной либо она сама, либо ее отрицание выводятся из , то выполняющий набор значений определен однозначно, и надо только проверить, что он действительно будет выполняющим. А если для каких-то переменных нельзя вывести ни их, ни их отрицание, то мы пополним наш набор так, чтобы они, как теперь модно говорить, "определились".

Проведем это рассуждение подробно. Рассмотрим все переменные, входящие в какие-либо формулы из множества ; обозначим множество этих переменных через . Зафиксируем это множество и до конца доказательства теоремы о полноте будем рассматривать только формулы с переменными из множества , не оговаривая этого особо.

Назовем непротиворечивое множество полным, если для любой формулы имеет место либо , либо (одновременно этого быть не может, так как непротиворечиво).

Утверждение теоремы о полноте очевидно следует из двух лемм:

Лемма 1. Всякое непротиворечивое множество содержится в непротиворечивом полном множестве .

Лемма 2. Для всякого непротиворечивого полного множества существует набор значений переменных (из , напомним), при котором все формулы из истинны.

Доказательство леммы 1. Основную роль здесь играет такое утверждение: если — непротиворечивое множество, а — произвольная формула, то хотя бы одно из множеств 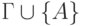и непротиворечиво. В самом деле, если оба множества 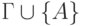и противоречивы, то и , но множество предполагалось непротиворечивым.

Если множество переменных конечно или счетно, то доказательство леммы легко завершить: множество всех формул тогда счетно, и просматривая их по очереди, мы можем добавлять к либо саму формулу, либо ее отрицание, сохраняя непротиворечивость. Получится, очевидно, полное множество. Чуть менее очевидна его непротиворечивость: оно было непротиворечиво на каждом шаге, но почему предельное множество (объединение возрастающей последовательности) будет непротиворечиво? Дело в том, что в выводе двух противоречащих друг другу формул может быть задействовано только конечное число формул из (по определению выводимости: вывод есть конечная последовательность формул). Поэтому все эти формулы должны появиться на некотором конечном шаге конструкции, а это невозможно (на всех шагах множество непротиворечиво).

Для случая произвольного набора переменных рассуждение можно завершить ссылкой на лемму Цорна: рассмотрим частично упорядоченное множество, элементами которого будут непротиворечивые множества формул, а порядком — отношение "быть подмножеством". Рассуждение предыдущего абзаца показывает, что всякая цепь в этом множестве имеет верхнюю границу (объединение линейно упорядоченного по включению семейства непротиворечивых множеств является непротиворечивым множеством). Следовательно, для любого непротиворечивого множества найдется содержащее его максимальное непротиворечивое множество. А оно обязано быть полным (иначе его можно расширить, добавив или ).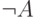

Лемма 1 доказана.

Доказательство леммы 2. Пусть — непротиворечивое полное множество. Тогда для каждой переменной (из множества ) ровно одна из формул и 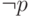выводима из . Если первая, будем считать переменную истинной, если вторая — ложной. Тем самым появляется некоторый набор значений переменных, и надо только проверить, что любая формула из при таких значениях переменных истинна. Это делается так: индукцией по построению формулы мы доказываем, что

Базис индукции (когда — переменная) обеспечивается определением истинности переменных. Для шага индукции используется та же лемма, что и при доказательстве полноты с помощью разбора случаев. Пусть, например, имеет вид 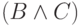. Тогда есть четыре возможности для истинности и . В одном из них (когда и истинны на ) по предположению индукции мы имеем 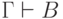и , откуда , то есть 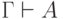. В другом ( истинна, ложна) предположение индукции дает 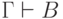и , откуда , то есть . Аналогично разбираются и все остальные случаи и логические связки. Лемма 2 доказана, и тем самым завершено доказательство теоремы 20.

Мы доказали, что всякое непротиворечивое множество формул совместно. Отсюда легко следует, что всякая тавтология является теоремой. В самом деле, если — тавтология, то множество несовместно, поэтому из 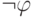выводится противоречие, поэтому , и по закону снятия двойного отрицания .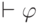

Кроме того, теорема о полноте во второй формулировке имеет такое очевидное следствие: