Полнота исчисления предикатов

Анализ доказательства позволяет сделать такое наблюдение:

Теорема 47. Непротиворечивое множество замкнутых формул конечной или счетной сигнатуры имеет счетную модель.

В самом деле, элементами построенной нами модели являются замкнутые термы, образованные из добавленных констант и функциональных символов сигнатуры. На каждом шаге добавляется счетное множество констант, поэтому всех констант счетное число, значит, и термов счетное число.

Аналогичное рассуждение с использованием свойств операций с мощностями (о которых можно прочесть в [6]) устанавливает такой факт:

Теорема 48. Всякое непротиворечивое множество формул сигнатуры имеет модель мощности (где 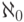обозначает счетную мощность, а — мощность сигнатуры).

Кстати, при доказательстве теорем 47 и 48 можно было бы сослаться на теорему Левенгейма-Сколема об элементарной подмодели (построить модель произвольной мощности, а потом уменьшить, если надо).

Возвратимся теперь к исходной формулировке теоремы о полноте.

Теорема 49 (полнота исчисления предикатов, слабая форма) Всякая общезначимая формула выводима в исчислении предикатов.

Пусть формула замкнута. Если она невыводима, то множество непротиворечиво и потому совместно. В его модели формула будет ложной, что противоречит предположению.

Что касается незамкнутых формул, то их общезначимость и выводимость равносильна общезначимости и выводимости их замыкания.

Как и в разделе "Второе доказательство теоремы о полноте", из теоремы о полноте можно вывести такое следствие:

Теорема 50. (компактность для исчисления предикатов). Пусть — множество замкнутых формул некоторой сигнатуры, и любое его конечное подмножество имеет модель. Тогда и само множество имеет модель.

В самом деле, по теореме о полноте (и корректности, если быть точным) наличие модели (совместность) равносильно непротиворечивости. А по определению противоречивость затрагивает лишь конечное число формул из .

101. Покажите, что теорема о полноте в сильной форме является следствием теоремы компактности и теоремы о полноте в слабой форме. (Указание: если множество не имеет модели, то его конечная часть не имеет модели, поэтому формула 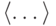общезначима, поэтому )

Прямое доказательство теоремы компактности (без использования понятия выводимости) мы дадим в следующей лекции.

Еще один важный результат, вытекающий из теоремы о полноте — совпадение синтаксического понятия выводимости и семантического понятия следования. Пусть дана некоторая сигнатура . Рассмотрим множество замкнутых формул этой сигнатуры (такие множества мы называем теориями в сигнатуре ) и еще одну замкнутую формулу . Говорят, что семантически следует из , если истинна во всякой модели теории , то есть во всякой интерпретации сигнатуры , где истинны все формулы из . (Обозначение: .)

Теорема 51.

Если , то .

Напротив, пусть не выводима из . Тогда теория непротиворечива и (в силу теоремы о полноте) имеет модель. Значит не следует из .

102. Какими нужно взять и в этой теореме, чтобы получить приведенные ранее формулировки теоремы о полноте? (Ответ: при (тождественно ложная формула) получаем сильную форму теоремы о полноте, при — слабую.)