Полнота исчисления предикатов

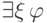Лемма 2. Пусть — непротиворечивое множество замкнутых формул, из которого выводится замкнутая формула . Пусть — константа, не встречающаяся ни в , ни в . Тогда множество останется непротиворечивым после добавления формулы .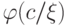

(Замечание. Здесь и далее, говоря о непротиворечивости и выводимости, мы не уточняем, в какой сигнатуре строятся выводы: все наши сигнатуры будут отличаться лишь набором констант, и лемма о добавлении констант.)

Доказательство леммы 2. Пусть становится противоречивым после добавления формулы 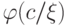. Отсюда следует (используем подходящую пропозициональную тавтологию), что отрицание этой формулы выводится из , то есть выводима формула , где — конъюнкция конечного числа формул из . По лемме о свежих константах выводима формула (напомним, что не входит ни в , ни в ). Контрапозиция дает формулу 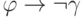, а правило Бернайса — формулу . По предположению формула 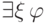выводима из , и множество оказывается противоречивым. Лемма 2 доказана.

100. Докажите такое усиление леммы 2: при добавлении в формулы 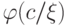(в предположениях леммы) множество выводимых из формул исходной сигнатуры (без константы ) не меняется.

Лемма 3. Пусть — непротиворечивое множество замкнутых формул сигнатуры . Тогда существует расширение сигнатуры новыми константами и непротиворечивое, полное и экзистенциально полное (в расширенной сигнатуре) множество замкнутых формул, содержащее .

Доказательство. Пусть сигнатура конечна или счетна. Тогда замкнутых формул вида 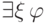, выводимых из , не более чем счетное число. К каждой из них по очереди будем применять лемму 2, вводя новую константу. Согласно этой лемме, на каждом шаге множество остается непротиворечивым, поэтому оно будет непротиворечивым и после добавления счетного числа формул (вывод противоречия затрагивает лишь конечное число формул).

Однако нельзя утверждать, что полученное множество будет экзистенциально полным в новой сигнатуре, поскольку про формулы вида 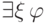с добавленными константами мы ничего не знаем. Пополним это множество, применив лемму 1, и повторим рассуждение: для каждой замкнутой выводимой формулы, начинающейся с квантора существования, введем новую константу и т. д.

Затем снова пополним его, снова добавим константы, снова пополним и так сделаем счетное число раз. Объединение всех полученных множеств будет непротиворечивым, полным и экзистенциально полным. В самом деле, оно непротиворечиво, так как противоречие должно выводиться из конечного числа формул (и поэтому должно появиться уже на конечном шаге). Оно полно: любая замкнутая формула содержит конечное число новых констант, поэтому на каком-то шаге пополнения она или ее отрицание станут выводимыми. Наконец, построенное множество экзистенциально полно по той же причине: всякая формула содержит конечное число новых констант, потому на следующем шаге для нее предусмотрена своя константа.

Что меняется, если сигнатура несчетна? Тогда мы уже не можем рассматривать все экзистенциальные формулы по очереди, и надо обрабатывать их все сразу. При этом противоречие не появится: в самом деле, оно использовало бы лишь конечное число добавленных формул, а для конечного числа все уже доказано.

После этого доказательство проходит как раньше (мы по-прежнему делаем счетное число чередующихся пополнений множества и расширений сигнатуры).

Лемма 3 доказана.

Последним шагом в доказательстве теоремы о полноте (всякое непротиворечивое множество замкнутых формул совместно) является такая лемма:

Лемма 4. Пусть — полное и экзистенциально полное множество замкнутых формул некоторой сигнатуры . Тогда существует интерпретация сигнатуры , в которой истинны все формулы из .

Мы уже говорили, как надо строить такую интерпретацию. Повторим это более подробно. Рассмотрим все замкнутые термы сигнатуры , то есть термы, не содержащие переменных, а только функциональные символы и константы. (Такие термы существуют, поскольку теория экзистенциально полна.) Это множество будет носителем интерпретации.

Как интерпретировать функциональные символы, понятно (это не зависит от множества ): если символ имеет валентность , то ему соответствует функция, которая отображает замкнутых термов 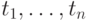в замкнутый терм 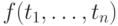. Константы (функциональные символы валентности ) интерпретируются сами собой.

Интерпретация предикатных символов такова. Пусть — предикатный символ валентности . Чтобы узнать, истинен ли соответствующий ему предикат на замкнутых термах 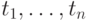, надо составить атомарную формулу 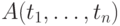и выяснить, что выводится из — сама эта формула или ее отрицание. (Здесь мы используем полноту.) В первом случае предикат будет истинным, во втором — ложным.

Индукцией по числу логических связок и кванторов в замкнутой формуле сигнатуры докажем такое утверждение:

Для атомарных формул это верно по построению интерпретации .

Для пропозициональных связок рассуждение ничем не отличается от приведенного в разделе "Второе доказательства теоремы о полноте". Нам нужно проверить, что выводимость из подчиняется тем же правилам, что и истинность:

Все эти свойства несложно доказать. Первое из них выражает полноту (и непротиворечивость — напомним, что по определению полная теория всегда непротиворечива) множества . Остальные свойства легко проверить, если иметь в виду, что все частные случаи пропозициональных тавтологий выводимы.

Пусть теперь формула имеет вид , где — формула с единственным параметром (или без параметров). Предположим, что она выводима из . Тогда в силу экзистенциальной полноты найдется константа , для которой 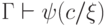. Формула 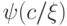имеет меньшее число логических связок, поэтому к ней можно применить предположение индукции и заключить, что она истинна в . Тогда формула истинна на оценке 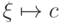, поэтому формула 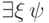истинна в .

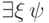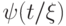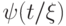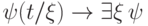Напротив, пусть формула истинна в . Тогда (по определению истинности) найдется элемент (замкнутый терм) , для которого истинна на оценке и потому формула истинна в . По предположению индукции формула выводима из . Осталось воспользоваться тем, что формула является аксиомой (напомним, подстановка замкнутого терма всегда корректна).

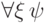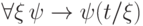Наконец, рассмотрим случай, когда формула имеет вид . Пусть она выводима из . Формула является аксиомой для любого замкнутого терма . Поэтому и формула 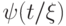выводима из . В ней меньше логических связок, чем в , поэтому по предположению индукции она истинна в . Значит, формула истинна на любой оценке 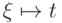, и потому формула 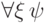истинна в .

Если формула 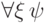не выводима из , то из выводится ее отрицание. Оно, как мы видели, доказуемо эквивалентно формуле . Поэтому в силу экзистенциальной полноты выводима формула для некоторой константы . Эта формула истинна, поэтому ложна при некотором значении переменной , так что формула 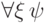ложна в .

Таким образом, мы доказали, что всякое непротиворечивое множество замкнутых формул имеет модель (расширив его до полного и экзистенциально полного множества, у которого есть модель из замкнутых термов).