Диаграммы
Лемма о расширении.
Если все 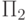 -следствия теории
-следствия теории  истинны в
интерпретации
истинны в
интерпретации  , то можно построить ее расширения
, то можно построить ее расширения 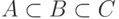 так, чтобы
так, чтобы  было моделью теории
было моделью теории  , а
, а  было
элементарным расширением
было
элементарным расширением  .
.
Прежде чем доказывать лемму о расширении, покажем (хотя это нам
и не понадобится), что сформулированное условие необходимо.
Пусть 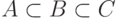 , причем
, причем  —
элементарное расширение
—
элементарное расширение  . Тогда любое
. Тогда любое 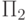 -утверждение,
истинное в
-утверждение,
истинное в  , истинно и в
, истинно и в  . В самом деле, пусть утверждение
. В самом деле, пусть утверждение  с бескванторной формулой
с бескванторной формулой  истинно в
истинно в  . Проверим его истинность в
. Проверим его истинность в  . Если оно
ложно при
. Если оно
ложно при 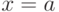 , то
, то 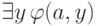 ложно и
в
ложно и
в  , и в
, и в  (элементарность расширения) и потому не может быть истинным
в
(элементарность расширения) и потому не может быть истинным
в  (поскольку всякое
(поскольку всякое  из
из  лежит и
в
лежит и
в  ).
).
Доказательство леммы о расширении. Что требуется от данного
расширения  интерпретации
интерпретации  , чтобы можно было
построить
, чтобы можно было
построить  с требуемыми свойствами? Свойства эти состоят в том, что
с требуемыми свойствами? Свойства эти состоят в том, что  должно быть моделью теории
должно быть моделью теории  и расширением
интерпретации
и расширением
интерпретации  . Как раз про это говорит
теорема 70, надо лишь в качестве
. Как раз про это говорит
теорема 70, надо лишь в качестве  в этой теореме взять нашу сигнатуру
в этой теореме взять нашу сигнатуру  с добавленными
константами для
с добавленными
константами для  (мы обозначали ее
(мы обозначали ее 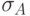 ), а в
качестве теории
), а в
качестве теории  из теоремы 70 взять
из теоремы 70 взять  , то есть множество всех истинных в
, то есть множество всех истинных в  формул
с константами из
формул
с константами из  .
.
Применяя указанный в теореме 70 критерий, можно сформулировать утверждение, которое нам осталось доказать,
так: найдется модель  теории
теории  , которая является
расширением
, которая является
расширением  и в которой истинны все
и в которой истинны все 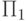 -формулы
сигнатуры
-формулы
сигнатуры 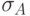 , выводимые из
, выводимые из  . Вспоминая
метод диаграмм, можно сказать, что нас интересует совместность
теории
. Вспоминая
метод диаграмм, можно сказать, что нас интересует совместность
теории  с
с  и со всеми
и со всеми 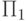 -
следствиями теории
-
следствиями теории  в сигнатуре
в сигнатуре 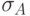 . В данном случае
. В данном случае  можно и не упоминать явно, так как оно содержится в
можно и не упоминать явно, так как оно содержится в  .
.
Итак, осталось доказать, что теория  совместна со всеми
совместна со всеми 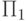 -формулами с константами из
-формулами с константами из  , истинными
в
, истинными
в  . Если это не так, из
. Если это не так, из  выводится отрицание какой-то из этих
формул, то есть некоторая
выводится отрицание какой-то из этих
формул, то есть некоторая 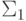 -формула
-формула
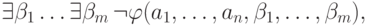
 . Константы
. Константы 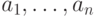 не входят в
теорию
не входят в
теорию  , поэтому из
, поэтому из  выводится и формула
выводится и формула
 формулой класса
формулой класса 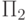 ,
ложной в
,
ложной в  , а таких формул не бывает по условию.
, а таких формул не бывает по условию.Лемма о расширении (а с ней и теорема Чэна-Лося-Сушко) доказана.
154. Докажите, что если формула устойчива относительно объединения
возрастающих цепей, то она выводимо эквивалентна некоторой 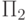 -формуле той же сигнатуры.
-формуле той же сигнатуры.
155. Покажите, что две интерпретации одной сигнатуры элементарно эквивалентны тогда и только тогда, когда они имеют изоморфные элементарные расширения.
