Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1280 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 8:

Методы расщепления
A
|
версия для печати
< Лекция 7 || Лекция 8: 123456 || Лекция 9 >
Аннотация: Лекция знакомит с идеями построения экономичных разностных схем для уравнений математической физики, основанных на методах покомпонентного расщепления (локально - одномерные схемы) и на принципах расщепления по физическим процессам
Ключевые слова: запись, производные, схема Кранка - Никольсон, устойчивость, метод прогонки, локально - одномерные схемы, операторы, аппроксимация, методы расщепления, диффузия, координаты, расщепление по физическим процессам, уравнения газовой динамики, энергия, метод переменных направлений, неявная разностная схема, обыкновенное дифференциальное уравнение

8.1. Понятие о методах расщепления

Рассмотрим дифференциальную задачу для уравнения в частных производных с постоянными коэффициентами:

$ {\frac{{\partial}u}{{\partial}t} + {\mathbf{A}}u = 0; x \in \Omega_x , t \in \Omega_t , \left. u\right|_\Gamma = u_\Gamma , u(t_0 ) = u_0 .} $ ( 8.1)

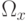Здесь оператор {\mathbf{A}} \ge 0 — положительный дифференциальный оператор с постоянными коэффициентами. В запись оператора \mathbf{A} входят производные по пространственным переменным. Для любого ненулевого элемента выполнено (\mathbf{A} \varphi, \varphi) \ge 0. \Gamma — граница области интегрирования \Omega _{x} ; \Lambda — разностный оператор, аппроксимирующий \mathbf{A}. Можно проверить, что разностное уравнение

$ {\frac{{u^{{n} + 1} - u^{n}}}{\tau} + {\mathbf{\Lambda}} \frac{{u^{{n} + 1} + u^{n}}}{2} = 0, u^0 = u_0} $ ( 8.2)

аппроксимирует (8.1) со вторым порядком по \tau ( схема Кранка - Никольсон ). Заметим, что (8.2) можно трактовать как результат попеременного применения явной и неявной схем первого порядка аппроксимации, записанных на интервалах [tn, t + 1/2], [tn + 1/2, tn + 1]

\begin{gather*} \frac{{u^{{n} + 1/2} - u^{n}}}{{{\tau}/2}} + {\mathbf{\Lambda}}u^{n} = 0, \\ {\frac{{u^{{n} + 1} - u^{{n} + 1/2}}}{{{\tau}/2}} + {\mathbf{\Lambda}}u^{{n} + 1} = 0.} \end{gather*} ( 8.3)

Исключая из уравнений (8.3) значения функции на промежуточном слое по времени (с полуцелым индексом), получим (8.2). Если \mathbf{A} = \mathbf{A}(t), то

$ {\frac{{u^{{n} + 1} - u^{{n}}}}{\tau} + {\mathbf{\Lambda}}^{n} \frac{{u^{{n} + 1} + u^{{n}}}}{{2}} = 0} $ ( 8.4)

при этом разностный оператор также является положительным:

(\Lambda_nu, u) \ge 0,

а решение на следующем слое по времени может быть записано в операторном виде следующим образом:

$ u^{{n} + 1} = ({\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}^{n} )^{- 1}({\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}^{n})u^{n}, $

или

u^{{n} + 1} = {\mathbf{T}}^{n} u^{n},

где

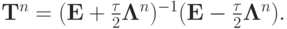
$ {\mathbf{T}}^{n} = ({\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}^{n} )^{- 1}({\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}^{n} ). $

Для доказательства устойчивости полученного разностного уравнения умножим скалярно (8.4) на (un + un + 1)/2, получим

$ {\frac{(u^{{n} + 1}, u^{{n} + 1}) - (u^{{n}}, u^{{n}})} {2 \tau} + \left({\mathbf{\Lambda}}^{n} \frac{{u^{{n} + 1} + u^{{n}}}}{{2}}, \frac{{u^{{n} + 1} + u^{{n}}}}{{2}}\right) = 0} $ ( 8.5)

Так как в силу положительности разностного оператора {(\Lambda^{n}u, u) \ge 0}, то из (8.5}) следует, что $ \left\| {u^{{n} + 1}\right\| \le \left\| {u^{n}}\right\|, $ чем и обеспечена устойчивость схемы. Если разностный оператор \Lambda (пространственные разности) выбран в виде полусуммы разностных операторов на верхнем и нижнем слоях по времени

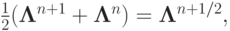
$ \frac{1}{2}({\mathbf{\Lambda}}^{{n} + 1} + {\mathbf{\Lambda}}^{n} ) = {\mathbf{\Lambda}}^{{n} + 1/2}, $
то схема имеет второй порядок аппроксимации по \tau.

8.2. Метод расщепления первого и второго порядка точности по tau

8.2.1. Локально - одномерные схемы

Положим, что дифференциальный оператор \mathbf{A} и соответствующий ему разностный оператор \Lambda можно представить в виде суммы операторов, каждый из которых включает производные лишь по одной пространственной переменной и разности лишь вдоль одного направления соответственно. Всего пространственных направлений N. Такие дифференциальные и разностные операторы будем называть локально - одномерными. И дифференциальный, и разностный операторы записываются в виде суммы локально - одномерных:

{\mathbf{A}} = \sum\limits_{{i} = 1}^{N}{{\mathbf{A}}_i }, {\mathbf{\Lambda}} = \sum\limits_i^{N}{{\mathbf{\Lambda}}_i }.

Для однородной задачи можно выписать схему расщепления по направлениям:

\begin{gather*} \frac{u^{n + 1/N} - u^n}{\tau} + {\mathbf{\Lambda}}_1 u^{n + 1/N} = 0, \\ \frac{u^{n + 2/N} - u^{n + 1/N}}{\tau} + {\mathbf{\Lambda}}_2 u^{n + 2/N} = 0, \\ \ldots \\ \frac{u^{n + 1} - u^{n + (N - 1)/N}}{\tau} + {\mathbf{\Lambda}}_n u^{{n} + 1} = 0. \end{gather*}

Получена система разностных уравнений, каждое из которых не аппроксимирует исходное дифференциальное, но может быть легко решено (методом прогонки вдоль соответствующего направления, если разностные операторы содержат лишь первые и вторые разности). Тем не менее, последовательно примененные друг за другом, они дают на следующем слое по времени решение с разумной точностью. Говорят, что имеет место суммарная аппроксимация — результирующий оператор послойного перехода получился аппроксимирующим. Описанный выше способ называется иногда методом дробных шагов, и уже встречался при решении многомерного уравнения теплопроводности.

Для неоднородной задачи один из возможных вариантов схемы расщепления имеет вид

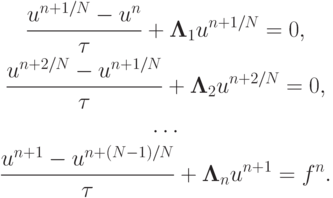
\begin{gather*} \frac{u^{n + 1/N} - u^n}{\tau} + {\mathbf{\Lambda}}_1 u^{{n} + 1/{N}} = 0, \\ \frac{u^{n + 2/N} - u^{n + 1/N}}{\tau} + {\mathbf{\Lambda}}_2 u^{n + 2/N} = 0, \\ \ldots \\ \frac{u^{n + 1} - u^{n + (N - 1) /N}}{\tau} + {\mathbf{\Lambda}}_n u^{{n} + 1} = f^{n} . \end{gather*}

Возможны и другие способы учета правой части, например, введение ее во все уравнения с весовыми множителями, которые подбираются из условий наилучшей суммарной аппроксимации (минимизации ошибки аппроксимации на следующем слое по времени).

Приведенные выше схемы расщепления по направлениям абсолютно устойчивы.

Дальше >>
< Лекция 7 || Лекция 8: 123456 || Лекция 9 >

Вопросы и ответы

вопросов: 0