Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1275 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 8:

Методы расщепления
A
|
версия для печати
< Лекция 7 || Лекция 8: 123456 || Лекция 9 >

8.3. Методы двуциклического покомпонентного расщепления

Для этих методов отсутствует требование коммутативности операторов \Lambda _{i}.

Будем рассматривать численное решение (8.1) не на одном шаге по времени, отрезке [tn, tn + 1], а на двух последовательных шагах [tn - 1, tn + 1]. Пусть теперь разностные локально - одномерные операторы зависят явно от времени, тогда они определены в середине отрезка 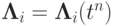{\mathbf{\Lambda}}_i = {\mathbf{\Lambda}}_i (t^{n} ). Запишем схему расщепления:

\begin{gather*} \frac{{u^{{n} - 1/2} - u^{{n} - 1}}}{\tau} + {\mathbf{\Lambda}}_1 \frac{{u^{{n} - 1/2} + u^{{n} - 1}}}{2} = 0, \\ \frac{{u^{n} - u^{{n} - 1/2}}}{\tau} + {\mathbf{\Lambda}}_2 \frac{{u^{n} + u^{{n} - 1/2}}}{2} = 0, \\ \frac{{u^{{n} + 1/2} - u^{n}}}{\tau} + {\mathbf{\Lambda}}_2 \frac{{u^{{n} + 1/2} - u^{n}}}{2} = 0, \\ {\frac{{u^{{n} + 1} - u^{{n} + 1/2}}}{\tau} + {\mathbf{\Lambda}}_1 \frac{{u^{{n} + 1} - u^{{n} + 1/2}}}{2} = 0.} \end{gather*} ( 8.6)

В операторной форме этот метод записывается как u^{n + 1} = {\mathbf{T}}^{n}u^{n - 1}, где введено обозначение

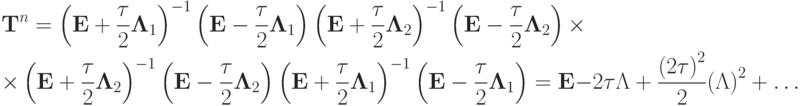
\begin{gather*} {\mathbf{T}}^{n} = \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_1}\right)^{- 1} \left({{\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}_1}\right) \left({{\mathbf{E}} + \frac{\tau}{2} {\mathbf{\Lambda}}_2}\right)^{- 1} \left({{\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}_2}\right) \times \\ \times \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_2}\right)^{- 1} \left({{\mathbf{E}}- \frac{\tau}{2}{\mathbf{\Lambda}}_2}\right) \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_1}\right)^{- 1} \left({{\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}_1}\right) = \mathbf{E}{- } 2 {\tau}{\Lambda}+ \frac{{(2 \tau)}^2}{2}{(\Lambda)}^2 + \ldots \end{gather*}

Если локально - одномерные операторы положительны 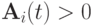{\mathbf{A}}_i (t) > 0, то при достаточной гладкости решения и элементов матриц {\mathbf{A}}_i (t) схема (8.6) абсолютно устойчива и аппроксимирует (8.1) со вторым порядком.

Для неоднородного дифференциального уравнения

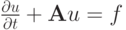
$ \frac{{\partial u}}{{\partial}t} + {\mathbf{A}}u = f $
разностная аппроксимация метода расщепления может быть представлена в виде

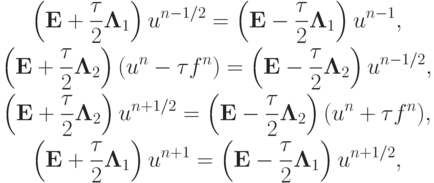
\begin{gather*} \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_1}\right)u^{n - 1/2} = \left({{\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}_1}\right)u^{n - 1}, \\ \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_2}\right)(u^{n} - {\tau}f^n) = \left({{\mathbf{E}} - \frac{\tau }{2}{\mathbf{\Lambda}}_2}\right)u^{n - 1/2}, \\ \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_2}\right)u^{n + 1/2} = \left({{\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}_2}\right)(u^{n} + {\tau}f^{n} ), \\ \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_1}\right)u^{n + 1} = \left({{\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}_1}\right)u^{n + 1/2}, \end{gather*}

где fn = f(tn).

В операторной форме записи решение неоднородной задачи имеет вид: 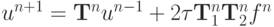u^{n + 1} = {\mathbf{T}}^{n} u^{n - 1} + 2 {\tau}{\mathbf{T}}_1^{n}{\mathbf{T}}_2^{n} f^{n}, где введены обозначения

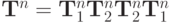
$ {\mathbf{T}}^{n} = {\mathbf{T}}_1^{n}{\mathbf{T}}_2^{n}{\mathbf{T}}_2^{n}{\mathbf{T}}_1^{n}
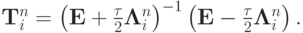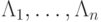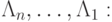
{\mathbf{T}}_i^{n} = \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_i^{n}}\right)^{- 1} \left({{\mathbf{E}} - \frac{\tau }{2}{\mathbf{\Lambda}}_i^{n}}\right). $ Представим разностную аппроксимацию неоднородного дифференциального уравнения с помощью последовательного применения операторов \Lambda _{1}, \dots , \Lambda _{n}, \Lambda _{n}, \dots , \Lambda _{1}:

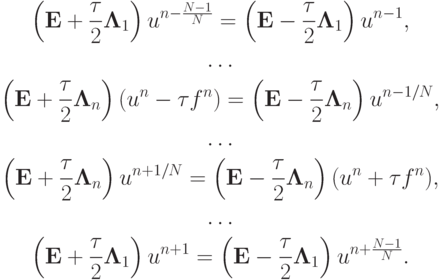
\begin{gather*} \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_1}\right)u^{n - \frac{N - 1}{N}} = \left({{\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}_1}\right)u^{n - 1}, \\ \ldots \\ \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_n }\right)(u^{n} - {\tau}f^{n} ) = \left({{\mathbf{E}} - \frac{\tau }{2}{\mathbf{\Lambda}}_n }\right)u^{n - 1/N}, \\ \ldots \\ \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_n }\right)u^{n + 1/N} = \left({{\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}_n }\right)(u^{n} + {\tau}f^{n} ), \\ \ldots \\ \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_1}\right)u^{n + 1} = \left({{\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}_1}\right)u^{n + \frac{{N - 1}}{N}} . \end{gather*}

Рассмотрим примеры использования метода двуциклического расщепления для некоторых задач математической физики.

Пример 1. Трехмерное нестационарное уравнение диффузии, область интегрирования — параллелепипед. Полагаем, что в вертикальном направлении (ось 0z ) коэффициент диффузии в вертикальной плоскости \gamma зависит от координаты, что характерно для задач геофизики, \mu — коэффициент диффузии в горизонтальной плоскости. Задача может быть представлена в виде

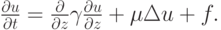
$ \frac{{\partial}u}{{\partial}t} = \frac{\partial }{{{\partial}z}} \gamma \frac{{\partial}u}{{{\partial}z}} + \mu \Delta u + f. $

Сведем решение рассматриваемой трехмерной задачи к последовательному решению трех одномерных задач. Первая задача имеет вид

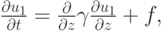
$ \frac{{{\partial}u_1}}{{\partial}t} = \frac{{\partial}}{{{\partial}z}} \gamma \frac{{{\partial}u_1}}{{{\partial}z}} + f, $

она описывает диффузию в вертикальной плоскости. Вторую и третью задачи запишем

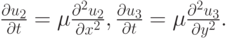
$ \frac{{{\partial}u_2}}{{\partial}t} = \mu \frac{{{\partial}^2 u_2}} {{{\partial}x^2}}, \frac{{{\partial}u_3 }}{{\partial}t} = \mu \frac{{{\partial}^2 u_3 }} {{{\partial}y^2}}. $

Теперь рассмотрим разностную аппроксимацию исходного дифференциального уравнения

\begin{gather*} \frac{{\partial}u}{{\partial}t} + ({\mathbf{\Lambda}}_1 + {\mathbf{\Lambda}}_2 + {\mathbf{\Lambda}}_3 )u = f, \mbox{ где} \\ {\mathbf{\Lambda}}_1 u = -\frac{\mu}{h_x^2}(u_{m, j, k + 1} - 2u_{mjk}+ u_{m, j, k - 1} ),\\ {\mathbf{\Lambda}}_2 u = -\frac{\mu}{h_y^2}(u_{m, j - 1, k} - 2u_{mjk} + u_{m, j + 1, k}),\\ {\mathbf{\Lambda}}_3 u = \frac{1}{{h_{z}}} \left[{- \frac{{\gamma_{m + 1/2, jk}}}{{h_{z}}}(u_{m + 1, jk} - u_{mjk} ) + \frac{{\gamma_{m - 1/2}}}{{h_{z}}} (u_{mjk} - u_{m - 1, jk} )}\right]. \end{gather*}

Разностная схема двуциклического покомпонентного расщепления приобретает вид

\begin{gather*} \frac{{u^{n + 1/6} - u^{n}}}{\tau} + {\mathbf{\Lambda}}_1 \frac{{u^{n + 1/6} + u^{n}}}{2} = 0, \\ \frac{{u^{n + 2/6} - u^{n + 1/6}}}{\tau} + {\mathbf{\Lambda}}_2 \frac{{u^{n + 2/6} + u^{n + 1/6}}}{2} = 0, \\ \frac{{u^{n + 3/6} - u^{n + 2/6}}}{\tau} + {\mathbf{\Lambda}}_3 \frac{{u^{n + 3/6} + u^{n + 2/6}}}{2} = \frac{{f^{n + 1/2}}}{2}, \\ \frac{{u^{n + 4/6} - u^{n + 3/6}}}{\tau} + {\mathbf{\Lambda}}_3 \frac{{u^{n + 4/6} + u^{n + 3/6}}}{2} = \frac{{f^{n + 1/2}}}{2}, \\ \frac{{u^{n + 5/6} - u^{n + 4/6}}}{\tau} + {\mathbf{\Lambda}}_2 \frac{{u^{n + 5/6} + u^{n + 4/6}}}{2} = 0, \\ \frac{{u^{n + 1} - u^{n + 5/6}}}{\tau} + {\mathbf{\Lambda}}_1 \frac{{u^{n + 1} + u^{n + 5/6}}}{2} = 0. \end{gather*}
Дальше >>
< Лекция 7 || Лекция 8: 123456 || Лекция 9 >

Вопросы и ответы

вопросов: 0