Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1276 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 8:

Методы расщепления
A
|
версия для печати
< Лекция 7 || Лекция 8: 123456 || Лекция 9 >

Пример 2. Сопряженное нестационарное уравнение переноса и диффузии

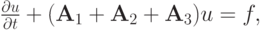
$ \frac{{\partial}u}{{\partial}t} + ({\mathbf{A}}_1 + {\mathbf{A}}_2 + {\mathbf{A}}_3 )u = f, $

где операторы определены как

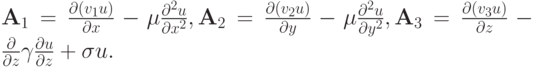
$ {\mathbf{A}}_1 = \frac{{{\partial}(v_{1} u)}}{{\partial}x} - \mu \frac{{{\partial}^2 u}}{{{\partial}x^2}}, {\mathbf{A}}_2 = \frac{{{\partial}(v_2u)}}{{\partial}y} - \mu \frac{{{\partial}^2 u}}{{{\partial}y^2}}, {\mathbf{A}}_3 = \frac{{{\partial}(v_3u)}}{{{\partial}z}} - \frac{{\partial}}{{{\partial}z}} \gamma \frac{{\partial}u}{{{\partial}z}} + {\sigma}u. $

Здесь v1, v2, v3 — компоненты вектора скорости, u — концентрация субстанции, \sigma — коэффициент поглощения субстанции внешней средой, \sigma > 0. Соответствующую схему расщепления представим в виде

\begin{gather*} \frac{{u^{n + 1/6} - u^{n}}}{\tau} + {\mathbf{\Lambda}}_1 \frac{{u^{n + 1/6} + u^{n}}}{2} = 0, \\ \frac{{u^{n + 2/6} - u^{n + 1/6}}}{\tau} + {\mathbf{\Lambda}}_2 \frac{{u^{n + 2/6} + u^{n + 1/6}}}{2} = 0, \\ \frac{{u^{n + 3/6} - u^{n + 2/6}}}{\tau} + {\mathbf{\Lambda}}_3 \frac{{u^{n + 3/6} + u^{n + 2/6}}}{2} = \frac{{f^{n + 1/2}}}{2}, \\ \frac{{u^{n + 4/6} - u^{n + 3/6}}}{\tau} + {\mathbf{\Lambda}}_3 \frac{{u^{n + 4/6} + u^{n + 3/6}}}{2} = \frac{{f^{n + 1/2}}}{2}, \\ \frac{{u^{n + 5/6} - u^{n + 4/6}}}{\tau} + {\mathbf{\Lambda}}_2 \frac{{u^{n + 5/6} + u^{n + 4/6}}}{2} = 0, \\ \frac{{u^{n + 1} - u^{n + 5/6}}}{\tau} + {\mathbf{\Lambda}}_1 \frac{{u^{n + 1} + u^{n + 5/6}}}{2} = 0, \end{gather*}

где разностные операторы аппроксимируют соответствующие локально - одномерные дифференциальные операторы. Так для рассматриваемой задачи

\begin{gather*} {\mathbf{\Lambda}}_1 u = - \frac{\mu }{{h_x^2}}(u_{m + 1, jk} - 2u_{mjk} + u_{m - 1j, k} ) + \frac{{(v_1 u)_{m + 1, jk} - (v_1 u)_{m - 1, jk}}}{{2h_x }}, \\ {\mathbf{\Lambda}}_2 u = - \frac{\mu }{{h_y^2}}(u_{m, j + 1, k} - 2u_{mjk} + u_{m, j - 1, k} ) + \frac{{(v_2 u)_{m, j + 1, k} - (v_2 u)_{m, j - 1, k}}}{{2h_y}}, \\ {\mathbf{\Lambda}}_3 u = \frac{1}{{h_{z}}} \left[{- \frac{{\gamma_{m + 1/2, jk}}}{{h_{z}}}(u_{m + 1, jk} - u_{mjk} ) + \frac{{\gamma_{m - 1/2}}}{h}(u_{mjk} - u_{m - 1, jk} )}\right] + \\ + \frac{{(v_3 u)_{m, j, k + 1} - (v_3 u)_{m, j, k - 1}}}{{2h_{z}}} + {\sigma}u_{mjk} . \end{gather*}

Отметим, что в рассматриваемой задаче на каждом этапе может быть проведено расщепление и по физическим процессам. Для простоты рассмотрим двухмерное уравнение конвекции - диффузии

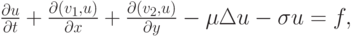
$ \frac{{\partial}u}{{\partial}t} + \frac{{{\partial}(v_1 , u)}} {{\partial}x} + \frac{{{\partial}(v_2 , u)}}{{\partial}y} - \mu \Delta u - {\sigma}u = f, $

в котором компоненты скорости движения среды v1, v2 удовлетворяют уравнению неразрывности:

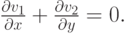
$ \frac{{{\partial}v_1}}{{\partial}x} + \frac{{{\partial}v_2}} {{\partial}y} = 0. $

Первый этап расщепления задачи по физическим процессам связан с переносом, на нем решается разностный аналог уравнения

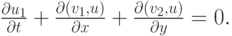
$ \frac{{{\partial}u_1}}{{\partial}t} + \frac{{{\partial}(v_1 , u)}} {{\partial}x} + \frac{{{\partial}(v_2 , u)}}{{\partial}y} = 0. $

Второй этап расщепления описывает процессы диффузии и поглощения субстанций

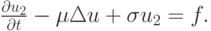
$ \frac{{{\partial}u_2}}{{\partial}t} - \mu \Delta u + {\sigma}u_2 = f. $

Пример 3. Расщепление по физическим процессам системы уравнений газовой динамики (метод крупных частиц).

Система

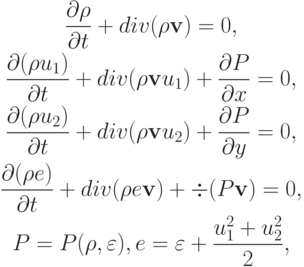
\begin{gather*} \frac{{\partial}\rho}{{\partial}t} + div ({\rho}{\mathbf{v}}) = 0, \\ \frac{{\partial}({\rho}u_1)}{{\partial}t} + div ({\rho}{\mathbf{v}}u_1 ) + \frac{{\partial P}}{{\partial}x} = 0, \\ \frac{{{\partial}({\rho}u_2 )}}{{\partial}t} + div ({\rho}{\mathbf{v}}u_2 ) + \frac{{\partial P}}{{\partial}y} = 0, \\ \frac{{{\partial}({\rho}e)}}{{\partial}t} + div ({\rho}e{\mathbf{v}}) + \div (P{\mathbf{v}}) = 0, \\ P = P({\rho}, \varepsilon ), e = \varepsilon + \frac{{u_1^2 + u_{2}^{2}}}{2}, \end{gather*}

u1 , u2 — компоненты вектора скорости \mathbf{v}, P — давление газа, \rho — плотность, \varepsilon — внутренняя энергия.

Первый (Эйлеров) этап. Измеряются лишь величины, относящиеся к ячейке в целом, а жидкость внутри каждой ячейки сетки считается моментально замороженной. Расчет производится по формулам, аппроксимирующим уравнения

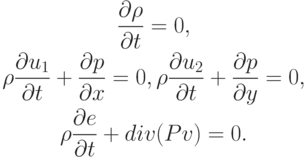
\begin{gather*} \frac{{{\partial}{\rho}}}{{\partial}t} = 0, \\ {\rho}\frac{{{\partial}u_1}}{{\partial}t} + \frac{{\partial}p}{{\partial}x} = 0, {\rho}\frac{{{\partial}u_2}}{{\partial}t} + \frac{{\partial}p}{{\partial}y} = 0, \\ {\rho}\frac{{\partial e}}{{\partial}t} + div (P{v}) = 0. \end{gather*}

На втором (Лагранжевом) этапе происходит движение газа массы через границы эйлеровых ячеек и перераспределение массы, импульса, энергии по пространству; определяются поля параметров течения газа. Аппроксимируется система уравнений

\begin{gather*} \frac{{{\partial}\rho }}{{\partial}t} + div ({\rho}{\mathbf{v}}) = 0, \\ \frac{{{\partial}({\rho}u_1 )}}{{\partial}t} + div ({\rho}u_1 {\mathbf{v}}) = 0, \frac{{{\partial}({\rho}u_2 )}}{{\partial}t} + div ({\rho}u_2 {\mathbf{v}}) = 0, \\ \frac{{{\partial}({\rho}e)}}{{\partial}t} + div ({\rho}e{\mathbf{v}}) = 0. \end{gather*}
Дальше >>
< Лекция 7 || Лекция 8: 123456 || Лекция 9 >

Вопросы и ответы

вопросов: 0