Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 8:

Методы расщепления
A
|
версия для печати
< Лекция 7 || Лекция 8: 123456 || Лекция 9 >

8.4. Методы расщепления с факторизацией оператора

8.4.1. Факторизованная схема расщепления

Пусть для решения дифференциальной задачи

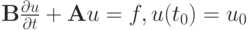
$ \mathbf{B} \frac{{\partial}u}{{\partial}t} + \mathbf{A}u = f, u(t_0 ) = u_0 $

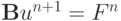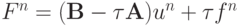используется разностная схема {\mathbf{B}}u^{n + 1} = F^{n}, где F^{n} = ({\mathbf{B}} - {\tau}{\mathbf{A}})u^{n} + {\tau}f^{n}, n = 0, 1, ... Пусть для вычисления Fn затрачивается O(N) действий, число арифметических операций пропорционально числу узлов сетки N. Такие разностные операторы называются экономичными.

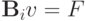Пусть \mathbf{B}_i (i = 1, 2, ..., N) - экономичные разностные операторы, такие, что {\mathbf{B}}_i v = F. Назовем схему разностной схемой с факторизованным оператором 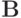\mathbf{B}, если возможно его представление в виде

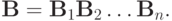
\mathbf{B} = \mathbf{B}_1 \mathbf{B}_2 \ldots \mathbf{B}_n.

Эта схема будет также экономичной, так как для решения разностного уравнения по - прежнему потребуется O(N) действий. В самом деле, решение уравнения

\mathbf{B}_1 \mathbf{B}_2 \ldots \mathbf{B}_n u^{n + 1} = F^{n}

может быть найдено в результате последовательного решения p уравнений

\begin{gather*} {\mathbf{B}}_1 u_1 = F^{n}, \\ {\mathbf{B}}_2 u_2 = u_1 , \\ {\mathbf{B}}_3 u_3 = u_2, \\ \ldots \\ {\mathbf{B}}_i u_i = u_{i - 1}, \end{gather*}

здесь i = 2, 3, ..., N. Тогда un + 1 = un. В записи задачи введены обозначения

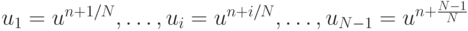
$ u_1 = u^{n + 1/N}, \ldots , u_i = u^{n + i/N}, \ldots , u_{N - 1} = u^{n + \frac{{N - 1}}{N}} $
— промежуточные значения.

Схемы с факторизованным оператором иногда называются также факторизованными схемами. Устойчивая схема с факторизованным оператором 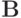\mathbf{B}, которая представляет собой произведение конечного числа операторов 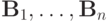\mathbf{B}_1, \ldots , \mathbf{B}_n, является экономичной схемой.

Пример. Метод переменных направлений (продольно - поперечная схема). Приведем запись схемы для решения линейного двумерного уравнения теплопроводности. Расчетные формулы есть

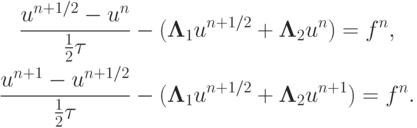
\begin{gather*} \frac{{u^{n + 1/2} - u^{n}}}{{{{1 \over 2}} \tau }} - ({\mathbf{\Lambda}}_1 u^{n + 1/2} + {\mathbf{\Lambda}}_2 u^{n} ) = f^{n}, \\ \frac{{u^{n + 1} - u^{n + 1/2}}}{{{{1 \over 2}} {\tau}}} - ({\mathbf{\Lambda}}_1 u^{n + 1/2} + {\mathbf{\Lambda}}_2 u^{n + 1} ) = f^{n} . \end{gather*}

Тогда, исключая un + 1/2, получим в операторной форме записи

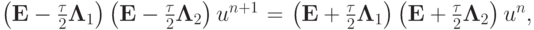
$ \left(\mathbf{E} - \frac{\tau}{2}\mathbf{\Lambda}_1\right) \left(\mathbf{E} - \frac{\tau}{2}\mathbf{\Lambda}_2\right) u^{n + 1} = \left(\mathbf{E} + \frac{\tau}{2}\mathbf{\Lambda}_1\right) \left(\mathbf{E} + \frac{\tau}{2} \mathbf{\Lambda}_2\right) u^{n}, $

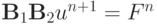или \mathbf{B}_1\mathbf{B}_2u^{n + 1} = F^{n}, где

$ {\mathbf{B}}_1 = {\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}_1 $
,
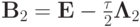
$ {\mathbf{B}}_2 = {\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}_2 $
,
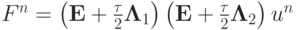
$ F^{n} = \left(\mathbf{E} + \frac{\tau}{2}\mathbf{\Lambda}_1\right) \left(\mathbf{E} + \frac{\tau}{2}\mathbf{\Lambda}_2\right)u^{n} $
. Разностная схема может быть представлена в виде факторизованный схемы расщепления:

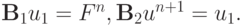
{\mathbf{B}}_1 u_1 = F^{n}, {\mathbf{B}}_2 u^{n + 1} = u_1.

8.4.2. Неявная схема расщепления с приближенной факторизацией

Рассмотрим неявную разностную схему

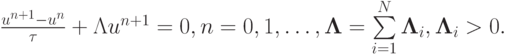$ {\frac{{u^{n + 1} - u^{n}}}{\tau} + {\Lambda}u^{n + 1} = 0, n = 0, 1, \ldots , {\mathbf{\Lambda}} = \sum\limits_{i = 1}^{N}{{\mathbf{\Lambda}}_i }, \mathbf{\Lambda}_i > 0.} $ ( 8.7)

Представим разностную схему (8.7) в виде

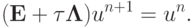{({\mathbf{E}} + {\tau}{\mathbf{\Lambda}})u^{n + 1} = u^{n} .} ( 8.8)

Факторизуем разностную схему (8.8) приближенно с точностью до членов порядка 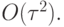O(\tau ^{2}). Для этого заменим в (8.8) оператор 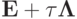{\mathbf{E}} + {\tau}{\mathbf{\Lambda}} на факторизованный

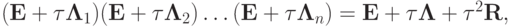
({\mathbf{E}} + \tau {\mathbf{\Lambda}}_1 )({\mathbf{E}} + {\tau}{\mathbf{\Lambda}}_2 ) \ldots ({\mathbf{E}} + {\tau}{\mathbf{\Lambda}}_n ) = {\mathbf{E}} + {\tau}{\mathbf{\Lambda}} + {\tau}^2 {\mathbf{R}},

где введено обозначение

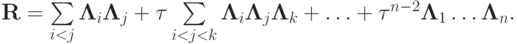
{\mathbf{R}} = \sum\limits_{i < j}{{\mathbf{\Lambda}}_i {\mathbf{\Lambda}}_j + {\tau}\sum\limits_{i < j < k}{{\mathbf{\Lambda}}_i }}{\mathbf{\Lambda}}_j {\mathbf{\Lambda}}_k + \ldots + {\tau}^{n - 2}{\mathbf{\Lambda}}_1 \ldots {\mathbf{\Lambda}}_n.

Врезультате приходим к неявной схеме с приближенной факторизацией

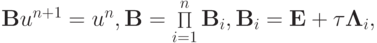
{\mathbf{B}}u^{n + 1} = u^{n}, \mathbf{B} = {\mathop \Pi\limits_{i = 1}^{n}{\mathbf{B}_i}}, {\mathbf{B}}_i = {\mathbf{E}} + {\tau}{\mathbf{\Lambda}}_i,

или

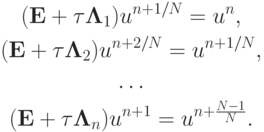
\begin{gather*} ({\mathbf{E}} + {\tau}{\mathbf{\Lambda}}_1 )u^{n + 1/N} = u^{n}, \\ ({\mathbf{E}} + {\tau}{\mathbf{\Lambda}}_2 )u^{n + 2/N} = u^{n + 1/N}, \\ \ldots \\ ({\mathbf{E}} + {\tau}{\mathbf{\Lambda}}_n )u^{n + 1} = u^{n + \frac{{N - 1}}{N}} . \end{gather*}

Эта схема абсолютно устойчива, имеет первый порядок аппроксимации.

Дальше >>
< Лекция 7 || Лекция 8: 123456 || Лекция 9 >

Вопросы и ответы

вопросов: 0