Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1281 / 292 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Лекция 8:

Методы расщепления
A
|
версия для печати
< Лекция 7 || Лекция 8: 123456 || Лекция 9 >

8.4.3. Метод "предиктор - корректор"

Основная идея методов типа "предиктор - корректор" заключается в следующем. На каждом отрезке [tn, tn + 1] задача решается в два приема: сначала по схеме первого порядка аппроксимации и со значительным запасом устойчивости находится решение в момент времени 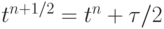t^{n + 1/2} = t^{n} + \tau /2 — предиктор. После этого на втором этапе расписывается исходное уравнение по схеме более высокого порядка аппроксимации (чаще всего, второго) — корректор. Основная идея семейств таких методов близка к идее построения методов типа Рунге - Кутты для обыкновенных дифференциальных уравнений.

Представим эту схему как следующую схему расщепления:

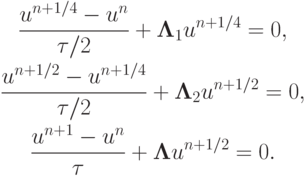
\begin{gather*} \frac{{u^{n + 1/4} - u^{n}}}{{{\tau}/2}} + {\mathbf{\Lambda}}_1u^{n + 1/4} = 0, \\ \frac{{u^{n + 1/2} - u^{n + 1/4}}}{{{\tau}/2}} + {\mathbf{\Lambda}}_2 u^{n + 1/2} = 0, \\ \frac{{u^{n + 1} - u^{n}}}{\tau} + {\mathbf{\Lambda}}u^{n + 1/2} = 0. \end{gather*}

Если в этой схеме расщепления исключить un + 1/4, то получим последовательность расчетных формул

\begin{gather*} \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_1}\right) \left({{\mathbf{E}} + \frac{\tau}{2} {\mathbf{\Lambda}}_2}\right)u^{n + 1/2} = {\varphi}^{n}, \\ \frac{{u^{n + 1} - u^{n}}}{\tau} + {\mathbf{\Lambda}}u^{n + 1/2} = 0, \end{gather*}

далее, исключив, 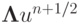{\mathbf{\Lambda}}u^{n + 1/2}, получим

$ \frac{{u^{n + 1} - u^{n}}}{\tau} + {\mathbf{\Lambda}} \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_2}\right)^{- 1} \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_1}\right)^{- 1}u^{n} = 0. $

Если для разностных операторов выполнены условия

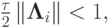
$ \frac{\tau}{2} \left\| {{\mathbf{\Lambda}}_i }\right\| < 1, $
{\mathbf{\Lambda}}_1 \ge 0, {\mathbf{\Lambda}}_2 \ge 0, а коэффициенты разностной схемы явно не зависят от времени, то при достаточной гладкости решения дифференциальной задачи разностная схема абсолютно устойчива и аппроксимирует исходную задачу со вторым порядком.

Далее рассмотрим случай, когда оператор \mathbf{\Lambda} представляется в виде суммы операторов \Lambda _{i}:

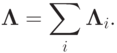
{\mathbf{\Lambda}} = \sum\limits_i {{\mathbf{\Lambda}}_i } .
Пусть все эти разностные операторы положительны. Метод "предиктор - корректор" можно записать в виде последовательности расчетных формул

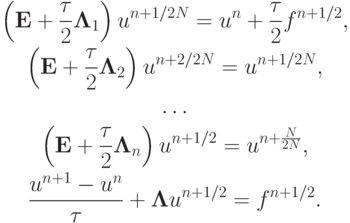
\begin{gather*} \left({{\mathbf{E}} + \frac{\tau}{2} {\mathbf{\Lambda}}_1}\right)u^{n + 1/2N} = u^{n} + \frac{\tau}{2}f^{n + 1/2}, \\ \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_2}\right)u^{n + 2/2N} = u^{n + 1/2N}, \\ \ldots \\ \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_n }\right)u^{n + 1/2} = u^{n + \frac{N}{{2N}}}, \\ \frac{{u^{n + 1} - u^{n}}}{\tau} + {\mathbf{\Lambda}}u^{n + 1/2} = f^{n + 1/2} . \end{gather*}

Эта последовательность после исключения промежуточных этапов сводится к одному разностному уравнению

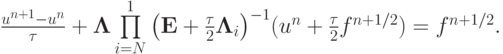
$ \frac{{u^{n + 1} - u^{n}}}{\tau} + {\mathbf{\Lambda}} \prod\limits_{i = N}^1 {\left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_i } \right)} ^{- 1} (u^{n} + \frac{\tau}{2}f^{n + 1/2} ) = f^{n + 1/2} . $

Приведем пример построения такой схемы. Для нестационарного трехмерного уравнения теплопроводности

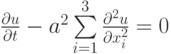
$ \frac{{\partial}u}{{\partial}t} - a^2 \sum\limits_{i = 1}^3 {\frac{{{\partial}^2 u}}{{{\partial}x_i^2}} = 0} $

получим следующую разностную схему типа "предиктор - корректор"

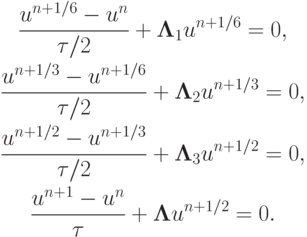
\begin{gather*} \frac{{u^{n + 1/6} - u^{n}}}{{{\tau}/2}} + {\mathbf{\Lambda}}_1 u^{n + 1/6} = 0, \\ \frac{u^{n + 1/3} - u^{n + 1/6}}{{\tau}/2} + {\mathbf{\Lambda}}_2 u^{n + 1/3} = 0, \\ \frac{u^{n + 1/2} - u^{n + 1/3}}{{\tau}/2} + {\mathbf{\Lambda}}_3 u^{n + 1/2} = 0, \\ \frac{{u^{n + 1} - u^{n}}}{\tau} + {\mathbf{\Lambda}}u^{n + 1/2} = 0. \end{gather*}

Далее, исключая промежуточные слои, получим схему, записанную в каноническом виде

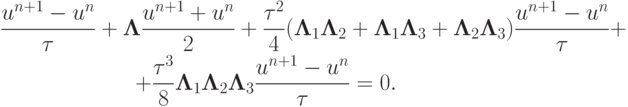
\begin{gather*} \frac{{u^{n + 1} - u^{n}}}{\tau} + {\mathbf{\Lambda}} \frac{{u^{n + 1} + u^{n}}}{2} + \frac{{{\tau}^2}}{4}({\mathbf{\Lambda}}_1 {\mathbf{\Lambda}}_2 + {\mathbf{\Lambda}}_1 {\mathbf{\Lambda}}_3 + {\mathbf{\Lambda}}_2 {\mathbf{\Lambda}}_3 ) \frac{{u^{n + 1} - u^{n}}}{\tau} + \\ + \frac{{{\tau}^3 }}{8}{\mathbf{\Lambda}}_1 {\mathbf{\Lambda}}_2 {\mathbf{\Lambda}}_3 \frac{{u^{n + 1} - u^{n}}}{\tau} = 0. \end{gather*}

Схема абсолютно устойчива (для коммутирующих операторов), имеет второй порядок аппроксимации по \tau и hi. Конечно, при практическом решении задач на компьютере используется именно последовательность разностных операторов. Канонический вид схемы удобен для ее теоретического исследования.

Дальше >>
< Лекция 7 || Лекция 8: 123456 || Лекция 9 >

Вопросы и ответы

вопросов: 0