Лемма Цорна и свойства операций

Свойства операций над мощностями

Теперь мы можем доказать несколько утверждений о мощностях.

Теорема 32. Если бесконечно, то множество равномощно .

Доказательство. Вполне упорядочим множество . Мы уже знаем , что всякий элемент множества однозначно представляется в ви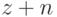де , где 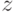- предельный элемент (не имеющий непосредственно предыдущего), а - натуральное число. Это означает, что равномощно , где - множество предельных элементов. (Тут есть небольшая трудность - последняя группа элементов конечна, если в множестве есть наибольший элемент. Но мы уже знаем, что добавление конечного или счетного множества не меняет мощности, так что этим можно пренебречь.)

Теперь утверждение теоремы очевидно: равномощно , то есть и тем самым (произведение счетных множеств счетно), то есть .

По теореме Кантора - Бернштейна отсюда следует, что промежуточные мощности (в частности, , а также любое произведение и конечного множества) совпадают с 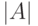. Еще одно следствие полезно выделить:

Теорема 33. Сумма двух бесконечных мощностей равна их максимуму.

Доказательство. Прежде всего напомним, что любые две мощности сравнимы (теорема 25). Пусть, скажем, 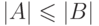. Тогда 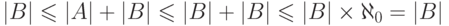(последнее неравенство - утверждение предыдущей теоремы). Остается воспользоваться теоремой Кантора- Бернштейна и заключить, что .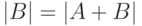

Теперь можно доказать более сильное утверждение.

Теорема 34. Если бесконечно, то равномощно .

Доказательство. Заметим, что для счетного множества (как, впрочем, и для континуума - но это сейчас не важно) мы это уже знаем. Поэтому в есть подмножество, равномощное своему квадрату.

Рассмотрим семейство всех таких подмножеств вместе с соответствующими биекциями. Элементами этого семейства будут пары 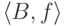, где - подмножество , а 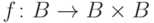- взаимно однозначное соответствие. Введем на этом семействе частичный порядок: 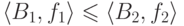, если и ограничение отображения на 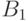совпадает с 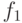(рис. рис.11.1).

Рис. 11.1.

Отображение 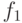- взаимно однозначное соответствие между малым квадратом и его стороной; добавляет к нему взаимно однозначное соответствие между 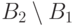и " уголком" .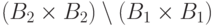

Теперь применим лемму Цорна. Для этого нужно убедиться, что любое линейно упорядоченное (в смысле описанного порядка) множество пар указанного вида имеет верхнюю границу. В самом деле, объединим все первые компоненты этих пар; пусть - их объединение. Как обычно, согласованность отображений (гарантируемая определением порядка) позволяет соединить отображения в одно. Это отображение (назовем его ) отображает в . Оно будет инъекцией: значения и 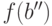при различных 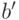и различны (возьмем большее из множеств, которым принадлежат 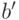и ; на нем является инъекцией по предположению). С другой стороны, является сюръекцией: для любой пары 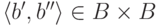возьмем множества, из которых произошли 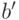и , выберем из них большее и вспомним, что мы имели взаимно однозначное соответствие между ним и его квадратом.