Ординалы
Как мы уже говорили, ординалом называется порядковый тип вполне упорядоченного множества, то есть класс всех изоморфных ему упорядоченных множеств (естественно, они будут вполне упорядоченными).
На ординалах естественно определяется линейный
порядок.
Чтобы сравнить два ординала  и
и  , возьмем
их
представители
, возьмем
их
представители  и
и  .
Применим теорему 22 и
посмотрим, какой из
трех случаев (
.
Применим теорему 22 и
посмотрим, какой из
трех случаев (  изоморфно начальному
отрезку
изоморфно начальному
отрезку  , отличному от всего
, отличному от всего  ;
множества
;
множества  и
и  изоморфны;
изоморфны;  изоморфно начальному отрезку
изоморфно начальному отрезку  ,
отличному от
всего
,
отличному от
всего  ) имеет место. В первом случае
) имеет место. В первом случае  ,
во втором
,
во втором  , в
третьем
, в
третьем 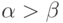 .
.
Мы отвлекаемся от трудностей, связанных с основаниями теории множеств (см. "лекцию 4" ); как формально можно оправдать наши рассуждения, мы еще обсудим. Пока что отметим некоторые свойства ординалов.
- Мы определили на ординалах линейный порядок. Этот порядок будет полным: любое непустое семейство ординалов имеет наименьший элемент (теорема 23; разница лишь в том, что мы не употребляли там слова "ординал", а говорили о представителях).
- Пусть
 - некоторый ординал. Рассмотрим начальный
отрезок
- некоторый ординал. Рассмотрим начальный
отрезок  в классе ординалов (образованный всеми ординалами,
меньшими
в классе ординалов (образованный всеми ординалами,
меньшими  в смысле
указанного порядка). Этот отрезок
упорядочен по типу
в смысле
указанного порядка). Этот отрезок
упорядочен по типу  (то есть изоморфен представителям
ординала
(то есть изоморфен представителям
ординала  ). В самом деле, пусть
). В самом деле, пусть  - один из
представителей ординала
- один из
представителей ординала  . Ординалы,
меньшие
. Ординалы,
меньшие  ,
соответствуют собственным (не совпадающим с
,
соответствуют собственным (не совпадающим с  ) начальным
отрезкам множества
) начальным
отрезкам множества  . Такие отрезки имеют вид
. Такие отрезки имеют вид 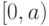 и тем
самым находятся во взаимно однозначном соответствии с
элементами множества
и тем
самым находятся во взаимно однозначном соответствии с
элементами множества  . (Легко проверить, что это соответствие
сохраняет порядок.)
. (Легко проверить, что это соответствие
сохраняет порядок.)Сказанное можно переформулировать так: каждый ординал упорядочен как множество меньших ординалов. (В одном из формальных построений теории ординалов каждый ординал равен множеству всех меньших ординалов.)
- Ординал называется непредельным, если существует непосредственно предшествующий ему (в смысле указанного порядка) ординал. Если такого нет, ординал называют предельным.
- Любое ограниченное семейство ординалов имеет точную верхнюю
грань (наименьший ординал, больший или равный всем ординалам
семейства). В самом деле, возьмем какой- то ординал
 ,
являющийся верхней границей. Тогда все ординалы семейства
изоморфны начальным отрезкам множества
,
являющийся верхней границей. Тогда все ординалы семейства
изоморфны начальным отрезкам множества  , представляющего
ординал
, представляющего
ординал  . Если среди этих отрезков есть само
. Если среди этих отрезков есть само  ,
то
,
то  будет точной верхней гранью (и наибольшим элементом
семейства). Если нет, то эти отрезки имеют вид
будет точной верхней гранью (и наибольшим элементом
семейства). Если нет, то эти отрезки имеют вид 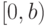 для
различных элементов
для
различных элементов 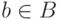 . Рассмотрим
множество
. Рассмотрим
множество 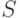 всех
таких элементов
всех
таких элементов  . Если
. Если 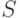 не ограничено
в
не ограничено
в  , то
, то  будет
точной верхней гранью. Если
будет
точной верхней гранью. Если 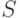 ограничено, то оно имеет
точную верхнюю грань
ограничено, то оно имеет
точную верхнюю грань  , и
, и 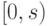 будет точной верхней
гранью
семейства.
будет точной верхней
гранью
семейства.
Можно сказать, что семейство ординалов- это как бы универсальное вполне упорядоченное семейство; любое вполне упорядоченное множество изоморфно некоторому начальному отрезку этого семейства. Поэтому мы немедленно придем к противоречию, если захотим рассмотреть множество всех ординалов (ведь для всякого вполне упорядоченного множества есть еще большее- добавим к нему новый элемент, больший всех предыдущих). Этот парадокс называется парадоксом Бурали- Форти.
124. Докажите, что точная верхняя грань счетного числа счетных ординалов счетна.
Как же рассуждать об ординалах, не впадая в противоречия? В
принципе можно заменять утверждения об ординалах утверждениями о
их представителях и воспринимать упоминания ординалов как "
вольность речи".
Другой подход (предложенный фон Нейманом)
применяется при аксиоматическом
построении теории множеств, и состоит он примерно в следующем:
мы объявляем каждый ординал равным множеству всех меньших
ординалов. Тогда минимальный ординал  (порядковый тип пустого
множества) будет пустым множеством
(порядковый тип пустого
множества) будет пустым множеством  , следующий за
ним ординал
, следующий за
ним ординал  (порядковый тип одноэлементного множества) будет
(порядковый тип одноэлементного множества) будет  , затем
, затем  ,
, 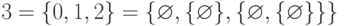 ,
,  и т.д
За ними следует ординал
и т.д
За ними следует ординал 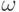 (порядковый тип множества
натуральных чисел), равный
(порядковый тип множества
натуральных чисел), равный 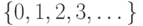 , потом
, потом 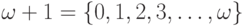 , потом
, потом 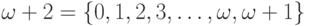 и т.д
и т.д
Мы не будем говорить подробно об аксиоматической теории множеств Цермело- Френкеля,
но два обстоятельства
следует иметь в виду.
Во-первых, в ней нет никаких объектов, кроме множеств, и есть аксиома экстенсиональности (или объемности ),
которая говорит, что два объекта, содержащие одни и те же
элементы, равны. Поэтому существует лишь один объект, не
содержащий элементов (пустое множество). Во-вторых, в ней есть аксиома фундирования }, которая говорит, что
отношение 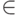 фундировано: во всяком множестве
фундировано: во всяком множестве  есть
элемент, являющийся
есть
элемент, являющийся 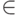 - минимальным, то есть
элемент
- минимальным, то есть
элемент 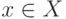 , для которого
, для которого 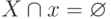 .
Отсюда следует, что
никакое множество
.
Отсюда следует, что
никакое множество  не может быть своим
элементом (иначе для множества
не может быть своим
элементом (иначе для множества  нарушалась бы аксиома
фундирования).
нарушалась бы аксиома
фундирования).
125. Выведите из аксиомы фундирования, что не существует множеств  ,
,  ,
, 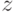 , для которых
, для которых 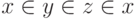 .
.
Философски настроенный математик объяснил бы смысл аксиомы фундирования так: множества строятся из ранее построенных множеств, начиная с пустого, и поэтому возможна индукция по построению (доказывая какое- либо свойство множеств, можно рассуждать индуктивно и предполагать, что оно верно для всех его элементов).
Теперь можно определить ординалы так. Будем говорить, что
множество  транзитивно, если всякий элемент
множества
транзитивно, если всякий элемент
множества  является подмножеством множества
является подмножеством множества  , то
есть если
из
, то
есть если
из 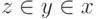 следует
следует 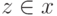 . Назовем ординалом транзитивное множество, всякий элемент
которого
транзитивен. Это требование гарантирует, что на элементах любого
ординала отношение
. Назовем ординалом транзитивное множество, всякий элемент
которого
транзитивен. Это требование гарантирует, что на элементах любого
ординала отношение 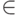 является (строгим)
частичным порядком.
является (строгим)
частичным порядком.
Аксиома фундирования гарантирует, что частичный порядок 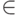 на
любом ординале является фундированным. После этого
по индукции можно доказать, что он является линейным (и,
следовательно, полным).
на
любом ординале является фундированным. После этого
по индукции можно доказать, что он является линейным (и,
следовательно, полным).
126. (а)
Используя определение ординала
как транзитивного множества с транзитивными элементами,
докажите, что элемент ординала есть ординал.
(б)
Пусть  - ординал (в смысле данного нами определения).
Докажите, что отношение
- ординал (в смысле данного нами определения).
Докажите, что отношение 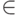 на нем является частичным порядком.
(в)
Докажите, что для любых элементов
на нем является частичным порядком.
(в)
Докажите, что для любых элементов 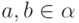 верно ровно
одно из трех соотношений: либо
верно ровно
одно из трех соотношений: либо  , либо
, либо 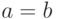 , либо
, либо  . (Указание: используйте двойную
индукцию по фундированному отношению
. (Указание: используйте двойную
индукцию по фундированному отношению 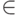 на
на  , а также аксиому экстенсиональности.)
(г)
Докажите, что один ординал изоморфен собственному начальному
отрезку другого тогда и только тогда, когда является его элементом.
(Таким образом, отношение
, а также аксиому экстенсиональности.)
(г)
Докажите, что один ординал изоморфен собственному начальному
отрезку другого тогда и только тогда, когда является его элементом.
(Таким образом, отношение  на ординалах как упорядоченных
множествах совпадает с отношением принадлежности.) Докажите, что
каждый ординал является множеством всех меньших его ординалов.
на ординалах как упорядоченных
множествах совпадает с отношением принадлежности.) Докажите, что
каждый ординал является множеством всех меньших его ординалов.
Заметим еще, что если каждый ординал есть множество всех меньших его ординалов, то точная верхняя грань множества ординалов есть их объединение.
Мы не будем подробно развивать этот подход и по- прежнему будем наивно представлять себе ординалы как порядковые типы вполне упорядоченных множеств.
Прежде чем перейти к сложению и умножению ординалов, отметим такое свойство:
Теорема 37.
Пусть  - подмножество вполне упорядоченного
множества
- подмножество вполне упорядоченного
множества  .
Тогда порядковый тип множества
.
Тогда порядковый тип множества  не
превосходит
порядкового
типа множества
не
превосходит
порядкового
типа множества  .
.
Доказательство.
Отметим сразу же, что равенство возможно, даже если  является
собственным подмножеством
является
собственным подмножеством  . Например, четные натуральные
числа имеют тот же порядковый тип
. Например, четные натуральные
числа имеют тот же порядковый тип 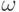 , что и все
натуральные числа.
, что и все
натуральные числа.
Рассуждая от противного, предположим, что порядковый тип
множества  больше. Тогда
больше. Тогда  изоморфно некоторому
начальному
отрезку множества
изоморфно некоторому
начальному
отрезку множества  , не совпадающему со всем
, не совпадающему со всем  .
Пусть
.
Пусть 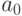 -
верхняя граница (в
-
верхняя граница (в  ) этого отрезка, а
) этого отрезка, а 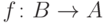 -
соответствующий изоморфизм. Тогда
-
соответствующий изоморфизм. Тогда  строго возрастает и
потому
строго возрастает и
потому 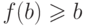 для всех
для всех 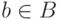 (теорема 17). В
частности,
(теорема 17). В
частности,  ,
но по предположению любое значение
,
но по предположению любое значение 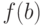 меньше
меньше 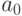 -
противоречие.
-
противоречие.
