Счетные множества
Множество называется счетным, если оно равномощно
множеству 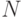 натуральных
чисел,
то есть если его можно
представить в виде
натуральных
чисел,
то есть если его можно
представить в виде  (здесь
(здесь  -
элемент, соответствующий числу
-
элемент, соответствующий числу  ; соответствие взаимно
однозначно, так что все
; соответствие взаимно
однозначно, так что все  различны).
различны).
Например, множество целых чисел 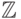 счетно, так как
целые числа можно расположить в последовательность
счетно, так как
целые числа можно расположить в последовательность  ,
,  ,
,  ,
, 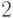 ,
,  ,
, 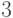 ,
, 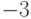 ,
, 
Теорема 2.
(а) Подмножество счетного множества конечно или счетно.
(б) Всякое бесконечное множество содержит счетное подмножество.
(в) Объединение конечного или счетного числа конечных или счетных множеств конечно или счетно.
Доказательство
(а) Пусть  - подмножество счетного множества
- подмножество счетного множества 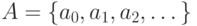 . Выбросим из последовательности
. Выбросим из последовательности 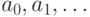 те члены, которые не принадлежат
те члены, которые не принадлежат  (сохраняя
порядок оставшихся). Тогда оставшиеся члены образуют либо
конечную последовательность (и тогда
(сохраняя
порядок оставшихся). Тогда оставшиеся члены образуют либо
конечную последовательность (и тогда  конечно), либо
бесконечную (и тогда
конечно), либо
бесконечную (и тогда  счетно).
счетно).
(б) Пусть  бесконечно. Тогда оно непусто и
содержит некоторый
элемент
бесконечно. Тогда оно непусто и
содержит некоторый
элемент  . Будучи бесконечным, множество
. Будучи бесконечным, множество  не
исчерпывается
элементом
не
исчерпывается
элементом  - возьмем какой - нибудь другой
элемент
- возьмем какой - нибудь другой
элемент 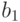 , и т.д.
Получится последовательность
, и т.д.
Получится последовательность 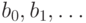 ;
построение не прервется ни на каком шаге, поскольку
;
построение не прервется ни на каком шаге, поскольку  бесконечно.
Теперь множество
бесконечно.
Теперь множество 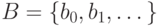 и будет искомым счетным
подмножеством. (Заметим, что
и будет искомым счетным
подмножеством. (Заметим, что  вовсе не обязано совпадать
с
вовсе не обязано совпадать
с  , даже если
, даже если  счетно.)
счетно.)
(в) Пусть имеется счетное число счетных множеств  Расположив элементы каждого из них слева направо в
последовательность (
Расположив элементы каждого из них слева направо в
последовательность ( 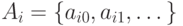 ) и
поместив эти последовательности друг под другом, получим
таблицу
) и
поместив эти последовательности друг под другом, получим
таблицу

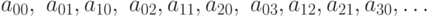
 не пересекались, то мы получили искомое
представление для их объединения. Если пересекались, то из
построенной последовательности надо выбросить повторения.
не пересекались, то мы получили искомое
представление для их объединения. Если пересекались, то из
построенной последовательности надо выбросить повторения.Если множеств конечное число или какие-то из множеств конечны, то в этой конструкции части членов не будет - и останется либо конечное, либо счетное множество.
29. Описанный
проход по диагоналям задает взаимно
однозначное соответствие между множеством всех пар натуральных
чисел (которое обозначается  ) и
) и 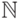 .
Любопытно, что это соответствие
задается простой формулой
(многочленом второй степени с рациональными коэффициентами).
Укажите этот многочлен.
.
Любопытно, что это соответствие
задается простой формулой
(многочленом второй степени с рациональными коэффициентами).
Укажите этот многочлен.
Замечание. В доказательстве утверждения (б)
теоремы 2 есть тонкий момент: на
каждом шаге мы должны выбрать один из оставшихся элементов
множества  ; такие элементы есть, но у нас нет никакого
правила, позволяющего такой выбор описать. При более формальном
построении теории множеств тут нужно сослаться на специальную
аксиому, называемую аксиомой выбора.
Законность этой
аксиомы вызывала большие споры в начале 20-го века, но
постепенно к ней привыкли, и эти споры сейчас почти не
воспринимаются. В середине века великий логик Курт
Гедель доказал, что аксиому выбора
нельзя опровергнуть, пользуясь остальными аксиомами теории
множеств, а в 1960-е годы американский математик
Пол Дж.Коэн доказал, что ее нельзя и вывести
из остальных аксиом. (Конечно, понимание этих утверждений
требует подробного изложения теории множеств как аксиоматической
теории.)
; такие элементы есть, но у нас нет никакого
правила, позволяющего такой выбор описать. При более формальном
построении теории множеств тут нужно сослаться на специальную
аксиому, называемую аксиомой выбора.
Законность этой
аксиомы вызывала большие споры в начале 20-го века, но
постепенно к ней привыкли, и эти споры сейчас почти не
воспринимаются. В середине века великий логик Курт
Гедель доказал, что аксиому выбора
нельзя опровергнуть, пользуясь остальными аксиомами теории
множеств, а в 1960-е годы американский математик
Пол Дж.Коэн доказал, что ее нельзя и вывести
из остальных аксиом. (Конечно, понимание этих утверждений
требует подробного изложения теории множеств как аксиоматической
теории.)
30. Такой же тонкий момент (хотя и менее очевидный) есть и в
доказательстве утверждения (в). Можете ли вы догадаться,
где он? (Ответ: мы знаем, что множества  счетны,
то есть что существует взаимно однозначное
соответствие между
счетны,
то есть что существует взаимно однозначное
соответствие между 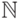 и
и  . Но нужно
выбрать и фиксировать эти соответствия, прежде чем
удастся построить соответствие между объединением всех
. Но нужно
выбрать и фиксировать эти соответствия, прежде чем
удастся построить соответствие между объединением всех  и
и 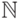 .)
.)
Еще несколько примеров счетных множеств:
- Множество
 рациональных
чисел
счетно. В самом деле,
рациональные числа представляются несократимыми дробями с целым
числителем и знаменателем. Множество дробей с данным знаменателем
счетно, поэтому
рациональных
чисел
счетно. В самом деле,
рациональные числа представляются несократимыми дробями с целым
числителем и знаменателем. Множество дробей с данным знаменателем
счетно, поэтому  представимо в виде
объединения счетного числа счетных множеств. Забегая вперед
(см.
"лекцию 4"
), отметим, что множество
представимо в виде
объединения счетного числа счетных множеств. Забегая вперед
(см.
"лекцию 4"
), отметим, что множество  всех
действительных чисел несчетно.
всех
действительных чисел несчетно. - Множество
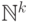 , элементами
которого являются наборы
из
, элементами
которого являются наборы
из  натуральных чисел, счетно. Это легко доказать индукцией
по
натуральных чисел, счетно. Это легко доказать индукцией
по  . При
. При  множество
множество  пар натуральных
чисел разбивается на счетное число счетных множеств
пар натуральных
чисел разбивается на счетное число счетных множеств 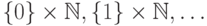 (элементами
(элементами  -го множества будут пары, первый член которых
равен
-го множества будут пары, первый член которых
равен  ).
Поэтому
).
Поэтому 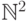 счетно. Аналогичным образом
множество
счетно. Аналогичным образом
множество 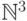 троек натуральных чисел разбивается на счетное
число множеств
троек натуральных чисел разбивается на счетное
число множеств  .
Каждое из них состоит из троек, первый член которых фиксирован и
потому равномощно множеству
.
Каждое из них состоит из троек, первый член которых фиксирован и
потому равномощно множеству 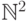 , которое счетно.
Точно так же можно перейти от счетности множества
, которое счетно.
Точно так же можно перейти от счетности множества 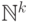 к счетности множества
к счетности множества  .
. - Множество всех конечных последовательностей натуральных чисел счетно. В самом деле, множество всех последовательностей данной длины счетно (как мы только что видели), так что интересующее нас множество разбивается на счетное число счетных множеств.
- В предыдущем примере не обязательно говорить о натуральных числах - можно взять любое счетное (или конечное) множество. Например, множество всех текстов, использующих русский алфавит (такой текст можно считать конечной последовательностью букв, пробелов, знаков препинания и т.п.), счетно; то же самое можно сказать о множестве (всех мыслимых) компьютерных программ и т.д.
- Число называют алгебраическим, если оно
является корнем
ненулевого многочлена с целыми коэффициентами. Множество
алгебраических чисел счетно, так как многочленов счетное число
(многочлен задается конечной последовательностью целых чисел -
его коэффициентов), а каждый многочлен имеет конечное число
корней (не более
 для многочленов степени
для многочленов степени  ).
). - Множество периодических дробей счетно.
В самом деле, такая дробь
может быть записана как конечная последовательность символов из
конечного множества (запятая, цифры, скобки); например,
дробь
 можно записать как
можно записать как 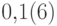 . А таких последовательностей счетное множество.
. А таких последовательностей счетное множество.
31. Докажите, что любое семейство непересекающихся интервалов на прямой конечно или счетно. (Указание: в каждом интервале найдется рациональная точка.)
32. (а) Докажите, что любое множество непересекающихся восьмерок на плоскости конечно или счетно. (Восьмерка - объединение двух касающихся окружностей любых размеров.) (б) Сформулируйте и докажите аналогичное утверждение для букв "Т".
33. Докажите, что множество точек строгого локального максимума любой функции действительного аргумента конечно или счетно.
Докажите, что множество точек разрыва неубывающей функции Действительного аргумента конечно или счетно.
