Теорема Кантора - Бернштейна
Продолжая эту конструкцию, мы получаем убывающую последовательность множеств
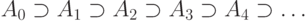
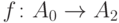 , при
котором
, при
котором  соответствует
соответствует 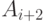 (иногда это
записывают так:
(иногда это
записывают так:  ). Формально можно описать
). Формально можно описать 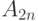 как
множество тех элементов, которые получаются из какого-то
элемента множества
как
множество тех элементов, которые получаются из какого-то
элемента множества 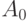 после
после  -кратного применения
функции
-кратного применения
функции  . Аналогичным образом
. Аналогичным образом  состоит из
тех и
только тех элементов, которые получаются из какого-то элемента
множества
состоит из
тех и
только тех элементов, которые получаются из какого-то элемента
множества  после
после  -кратного применения
функции
-кратного применения
функции  .
.Заметим, что пересечение всех множеств  вполне может быть
непусто: оно состоит из тех элементов, у которых
можно сколько угодно раз брать
вполне может быть
непусто: оно состоит из тех элементов, у которых
можно сколько угодно раз брать  - прообраз. Теперь можно сказать
так:
множество
- прообраз. Теперь можно сказать
так:
множество 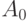 мы разбили на непересекающиеся слои
мы разбили на непересекающиеся слои 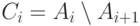 и на сердцевину
и на сердцевину  .
.
Слои  ,
, 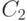 ,
, 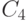 ,
,  равномощны (функция
равномощны (функция  осуществляет
взаимно однозначное соответствие между
осуществляет
взаимно однозначное соответствие между  и
и 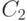 ,
между
,
между 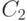 и
и 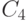 и т.д.):
и т.д.):
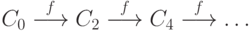
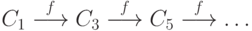
 на множестве
на множестве  осуществляет его перестановку (взаимно однозначное
соответствие с самим собой).
осуществляет его перестановку (взаимно однозначное
соответствие с самим собой).Теперь легко понять, как построить взаимно однозначное
соответствие  между
между 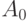 и
и  . Пусть
. Пусть 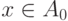 . Тогда
соответствующий ему элемент
. Тогда
соответствующий ему элемент  строится так:
строится так:  при
при 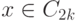 и
и 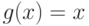 при
при  или
или 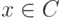 (см. рис. 3.4).
(см. рис. 3.4).
История этой теоремы (называемой также теоремой Шредера- Бернштейна) такова. Кантор формулирует ее без доказательства в 1883 году, обещая: " К этому я еще вернусь в одной более поздней работе и тогда выявлю своеобразный интерес этой общей теоремы". Однако этого обещания он не выполнил, и первые доказательства были даны Шредером (1896) и Бернштейном (1897). Как видно из работ и писем Кантора, он предполагал доказывать эту теорему одновременно с возможностью сравнить любые два множества (см. "Теорема Цермело" , теорема 25, но как именно - остается непонятным. (Работы Кантора по теории множеств и его письма переведены на русский язык ; все цитаты даются по этому изданию.)
Теорема Кантора-Бернштейна значительно упрощает доказательства равномощности: например, если мы хотим доказать, что бублик и шар в пространстве равномощны, то достаточно заметить, что из бублика можно вырезать маленький шар (гомотетичный большому), а из шара - маленький бублик.
45. Посмотрите на приведенные выше задачи, где требовалось доказать равномощность, и убедитесь, что во многих из них применение теоремы Кантора - Бернштейна сильно упрощает дело.
46. Докажите, что все геометрические фигуры, содержащие хотя бы кусочек прямой или кривой, равномощны.
47. Докажите, что если квадрат разбит на два множества, то хотя бы одно из них равномощно квадрату. (Указание. Если одна из частей содержит отрезок, то можно воспользоваться теоремой Кантора - Бернштейна. Если же, скажем, первая часть не содержит отрезков, то в каждом горизонтальном сечении квадрата есть точка второй части, и снова можно сослаться на теорему Кантора - Бернштейна.)

