Теорема Кантора - Бернштейна
48. Докажите, что если отрезок разбит на две части, то хотя бы одна из них равномощна отрезку.
То же самое доказательство можно изложить более
абстрактно (и избавиться от упоминания натуральных
чисел). Напомним, что 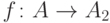 есть взаимно однозначное
соответствие между множеством
есть взаимно однозначное
соответствие между множеством  и его
подмножеством
и его
подмножеством  ,
а
,
а  - некоторое промежуточное множество. Назовем
множество
- некоторое промежуточное множество. Назовем
множество 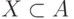 " хорошим", если оно содержит
" хорошим", если оно содержит  и замкнуто относительно
и замкнуто относительно  ,т.е.
,т.е.
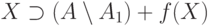
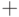 для объединения, поскольку объединяемые
множества заведомо не пересекаются). Легко проверить, что
пересечение любого семейства хороших множеств хорошее, поэтому
если мы пересечем все хорошие множества, то получим минимальное
по включению хорошее множество. Назовем его
для объединения, поскольку объединяемые
множества заведомо не пересекаются). Легко проверить, что
пересечение любого семейства хороших множеств хорошее, поэтому
если мы пересечем все хорошие множества, то получим минимальное
по включению хорошее множество. Назовем его  . Легко
проверить, что множество
. Легко
проверить, что множество 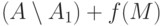 будет хорошим,
поэтому в силу минимальности
будет хорошим,
поэтому в силу минимальности  включение в определении
хорошего множества превращается в равенство:
включение в определении
хорошего множества превращается в равенство: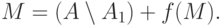
 .
Эта биекция совпадает с
.
Эта биекция совпадает с  внутри
внутри  и тождественна
вне
и тождественна
вне  .
.49. Проведите это рассуждение подробно.
Это рассуждение удобно при построении аксиоматической теории
множеств, так как в нем не нужны натуральные числа (которые
строятся далеко не сразу). Но по существу это то же самое
рассуждение, поскольку  есть
есть 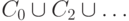
50. Пусть  - взаимно однозначное соответствие между
- взаимно однозначное соответствие между  и
некоторым подмножеством множества
и
некоторым подмножеством множества  , а
, а  - взаимно
однозначное соотвествие между
- взаимно
однозначное соотвествие между  и некоторым подмножеством
множества
и некоторым подмножеством
множества  . Докажите, что можно так разбить
множество
. Докажите, что можно так разбить
множество  на
непересекающиеся части
на
непересекающиеся части 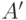 и
и 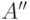 , а
множество
, а
множество  - на
непересекающиеся части
- на
непересекающиеся части  и
и 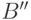 , что
, что  осуществляет
взаимно однозначное соответствие между
осуществляет
взаимно однозначное соответствие между 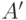 и
и  , а
, а  -
между
-
между 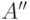 и
и 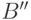 . (Указание: именно это мы фактически
установили
при доказательстве теоремы Кантора - Бернштейна.)
. (Указание: именно это мы фактически
установили
при доказательстве теоремы Кантора - Бернштейна.)
51. Докажите, что квадрат можно разбить на две части так, что из
подобных им частей можно сложить круг. Формально: квадрат можно
разбить на две части 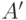 и
и 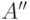 , а круг - на две части
, а круг - на две части  и
и 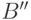 , для которых
, для которых 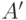 подобно
подобно  , а
, а 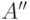 подобно
подобно 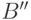 .
(Указание: воспользуйтесь предыдущей задачей.)
.
(Указание: воспользуйтесь предыдущей задачей.)
Теперь, имея в виду теорему Кантора - Бернштейна, вернемся к
вопросу о сравнении мощностей. Для данных множеств  и
и  теоретически имеются четыре возможности:
теоретически имеются четыре возможности:
-
 равномощно некоторой части
равномощно некоторой части  , а
, а  равномощно некоторой
части
равномощно некоторой
части  . (В этом случае, как мы знаем, множества равномощны.)
. (В этом случае, как мы знаем, множества равномощны.) -
 равномощно некоторой части
равномощно некоторой части  , но
, но  не равномощно никакой
части
не равномощно никакой
части  . В этом случае говорят, что
. В этом случае говорят, что  имеет
меньшую
мощность, чем
имеет
меньшую
мощность, чем  .
. -
 равномощно некоторой части
равномощно некоторой части  , но
, но  не равномощно никакой
части
не равномощно никакой
части  . В этом случае говорят, что
. В этом случае говорят, что  имеет
большую
мощность, чем
имеет
большую
мощность, чем  .
. - Ни
 не равномощно никакой части
не равномощно никакой части  ,
ни
,
ни  не равномощно
никакой части
не равномощно
никакой части  . Этот случай на самом деле невозможен, но мы
этого пока не знаем (см.
"Теорема Цермело"
).
. Этот случай на самом деле невозможен, но мы
этого пока не знаем (см.
"Теорема Цермело"
).
52. Докажите, что счетное множество имеет меньшую мощность, чем любое несчетное.
53. Проверьте аккуратно, что если  имеет меньшую мощность,
чем
имеет меньшую мощность,
чем  ,
а
,
а  имеет меньшую мощность, чем
имеет меньшую мощность, чем  , то
, то  имеет меньшую
мощность, чем
имеет меньшую
мощность, чем  (транзитивность сравнения мощностей).
(транзитивность сравнения мощностей).
Заметим, что мы уже долго говорим о сравнении мощностей, но
воздерживаемся от упоминания "мощности множества" как
самостоятельного объекта, а только сравниваем мощности разных
множеств. В принципе можно было бы определить мощность
множества  как класс всех множеств, равномощных
как класс всех множеств, равномощных  .
Такие
классы для множеств
.
Такие
классы для множеств  и
и  совпадают в том и только
том случае,
когда
совпадают в том и только
том случае,
когда  и
и  равномощны, так что слова " имеют
равную мощность" приобрели бы буквальный смысл. Проблема тут
в том, что таких множеств (равномощных множеству
равномощны, так что слова " имеют
равную мощность" приобрели бы буквальный смысл. Проблема тут
в том, что таких множеств (равномощных множеству  ) слишком
много, поскольку все на свете может быть их элементами. Их
насколько много, что образовать из них множество затруднительно,
это может привести к парадоксам (см.
"Теорема Кантора"
).
) слишком
много, поскольку все на свете может быть их элементами. Их
насколько много, что образовать из них множество затруднительно,
это может привести к парадоксам (см.
"Теорема Кантора"
).
Из этой ситуации есть несколько выходов. Самый простой - по-
прежнему говорить только о сравнении мощностей, но не о самих
мощностях. Можно также ввести понятие " класса" - такой
большой совокупности объектов, что ее уже нельзя считать
элементом других совокупностей (" если вы понимаете, о чем я
тут толкую" - добавила бы Сова из книжки о Винни- Пухе), и считать
мощностью множества  класс всех множеств,
равномощных
класс всех множеств,
равномощных  .
Еще один выход - для каждого
.
Еще один выход - для каждого  выбрать некоторое "
стандартное" множество, равномощное
выбрать некоторое "
стандартное" множество, равномощное  , и назвать его
мощностью множества
, и назвать его
мощностью множества  . Обычно в качестве стандартного
множества берут минимальный ординал, равномощный
. Обычно в качестве стандартного
множества берут минимальный ординал, равномощный  , - но это
построение уже требует более формального (аксиоматического)
построения теории множеств.
, - но это
построение уже требует более формального (аксиоматического)
построения теории множеств.
Кантор говорил о мощностях так (1895): " Мощностью
или кардинальным числом
множества  мы называем то
общее понятие, которое получается при помощи нашей активной
мыслительной способности из
мы называем то
общее понятие, которое получается при помощи нашей активной
мыслительной способности из  , когда мы абстрагируемся от
качества его различных элементов
, когда мы абстрагируемся от
качества его различных элементов  и от порядка их задания.
и от порядка их задания.  Так как из каждого отдельного элемента
Так как из каждого отдельного элемента  , когда мы отвлекаемся от качества, получается некая
" единица", то само кардинальное число оказывается
множеством, образованным исключительно из единиц, которое
существует как интеллектуальный образ или как проекция заданного
множества
, когда мы отвлекаемся от качества, получается некая
" единица", то само кардинальное число оказывается
множеством, образованным исключительно из единиц, которое
существует как интеллектуальный образ или как проекция заданного
множества  в наш разум".
в наш разум".
Так или иначе, мы будем употреблять обозначение 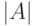 для
мощности множества
для
мощности множества  хотя бы как вольность речи:
хотя бы как вольность речи:  означает, что множества
означает, что множества  и
и  равномощны;
равномощны; 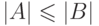 означает, что
означает, что  равномощно некоторому подмножеству
множества
равномощно некоторому подмножеству
множества  , а
, а 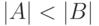 означает, что
означает, что  имеет
меньшую мощность, чем
имеет
меньшую мощность, чем 
