| Россия |
Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость
Аналогично можно получить выражение для невязки разностной схемы
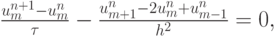
аппроксимирующей уравнение теплопроводности
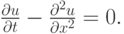
После соответствующих вычислений получим
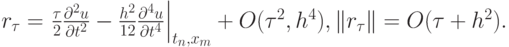
Таким образом, схема обладает первым порядком аппроксимации по 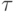 и вторым по h.
и вторым по h.
Определение 3. Говорят, что разностная задача является устойчивой, если из соотношений
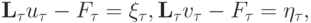
следует в смысле выбранной нормы

Теорема (П. Лакса - В.С.Рябенького). Решение линейной разностной задачи сходится к решению дифференциальной , если разностная задача устойчива и аппроксимирует дифференциальную задачу на ее решении. При этом порядок аппроксимации совпадает с порядком сходимости.
Дадим еще одно эквивалентное определение устойчивости разностной задачи, применимое лишь для линейных разностных операторов. Как будет видно ниже, даже для линейных дифференциальных задач возможно построение нелинейных разностных схем.
Определение 4. Линейная разностная задача устойчива, если при любой правой части  она имеет единственное решение
она имеет единственное решение 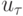 , причем
, причем 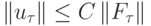 , и данная оценка равномерна по сеточным параметрам
, и данная оценка равномерна по сеточным параметрам 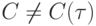 .
.
Покажем, что из устойчивости задачи в смысле второго определения следует ее устойчивость в смысле первого определения.
Вычтем из разностного уравнения 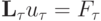 "возмущенное" разностное уравнение (положим для простоты
"возмущенное" разностное уравнение (положим для простоты  ):
):
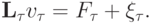
Получим в силу линейности разностного оператора

В силу определения 4 справедливо неравенство

откуда и следует справедливость в смысле определения 3 , так как 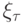 в этом неравенстве играет роль правой части, а
в этом неравенстве играет роль правой части, а  — искомой функции. Можно также показать справедливость обратного утверждения. Заметим, что в силу произвольности
— искомой функции. Можно также показать справедливость обратного утверждения. Заметим, что в силу произвольности 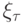 , из последнего неравенства следует единственность решения разностного уравнения.
, из последнего неравенства следует единственность решения разностного уравнения.
В теории разностных схем также вводится определение корректности разностной задачи.
Определение 5. Семейство разностных уравнений
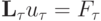
считается корректным, если:
- его решение существует и единственно при любых правых частях
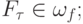
- существует константа C, независящая от
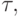 такая, что при любых
такая, что при любых  выполняется оценка
выполняется оценка 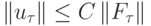 .
.
Первое условие эквивалентно существованию оператора 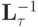 , второе — равномерной по
, второе — равномерной по 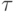 ограниченности
ограниченности 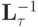 , т.е.
константа C является универсальной для всего семейства уравнений.
, т.е.
константа C является универсальной для всего семейства уравнений.
Заметим также, что условие 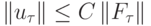 означает непрерывную равномерную по
означает непрерывную равномерную по 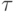 зависимость решения разностной задачи от правой части.
зависимость решения разностной задачи от правой части.
Это неравенство является введенным ранее определением устойчивости разностной задачи.
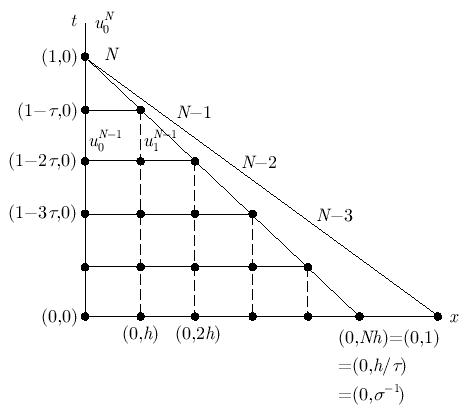
1.2.2. Необходимое условие сходимости разностной схемы Куранта, Фридрихса, Леви (условие КФЛ)
Рассмотрим разностное уравнение

аппроксимирующее задачу Коши для уравнения переноса
![$ \frac{{\partial}u}{{\partial}t} - \frac{{\partial}u}{{\partial}x} = 0, t \in [0, 1], u(0, x) = \varphi(x).](/sites/default/files/tex_cache/597f13f6b470e22f5e0e51dc7b0b404d.png)
Очевидно, что значение 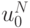 сеточной функции в точке (1, 0) выражается через значения
сеточной функции в точке (1, 0) выражается через значения 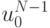 и
и 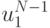 в точках
в точках 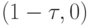 ,
, 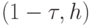 . В свою очередь, значения
. В свою очередь, значения 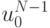 и
и 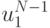 находятся по значениям сеточной функции
находятся по значениям сеточной функции 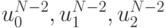 в точках
в точках 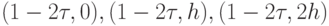 , значения сеточной функции
, значения сеточной функции 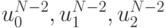 находятся по значениям
находятся по значениям 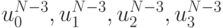 в точках
в точках 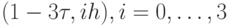 , и т.д. Значение сеточной функции
, и т.д. Значение сеточной функции 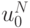 выражается через значение
выражается через значение 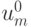 решения в
точках расчетной сетки
решения в
точках расчетной сетки  Все эти точки лежат на отрезке
Все эти точки лежат на отрезке ![[0, h/\tau ]](/sites/default/files/tex_cache/8598b5edd16e2c3c8e238064966c8e28.png) или
или ![[0, \sigma ^{ - 1}]](/sites/default/files/tex_cache/0eb8e348ea2a05584df1a2ca480d99b1.png) оси t = 0, на которой задано начальное условие
оси t = 0, на которой задано начальное условие 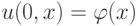 исходной дифференциальной задачи. Значение
исходной дифференциальной задачи. Значение 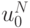 не зависит от значения функции
не зависит от значения функции 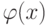 при x, лежащих вне отрезка
при x, лежащих вне отрезка ![[0, \sigma ^{ - 1}]](/sites/default/files/tex_cache/0eb8e348ea2a05584df1a2ca480d99b1.png) .
.
Из курса обыкновенных дифференциальных уравнений известно, что решением однородного уравнения переноса является функция 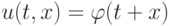 , сохраняющая свое значение вдоль характеристики t + x = const, и, в частности, на прямой t + x = 1, проходящей через точки (1, 0), (0, 1) , см. рис. 1.4.
, сохраняющая свое значение вдоль характеристики t + x = const, и, в частности, на прямой t + x = 1, проходящей через точки (1, 0), (0, 1) , см. рис. 1.4.
Таким образом, при  область зависимости
решения дифференциальной задачи для
область зависимости
решения дифференциальной задачи для 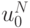 , являющаяся точкой (0, 1), не входит в отрезок
, являющаяся точкой (0, 1), не входит в отрезок 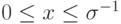 . В случае
. В случае  и
и 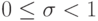 сходимость решения разностной задачи к решению дифференциальной отсутствует. Разумеется, приведенные рассуждения не носят характера доказательства, а лишь косвенно объясняют, почему не следует ожидать сходимости при
сходимость решения разностной задачи к решению дифференциальной отсутствует. Разумеется, приведенные рассуждения не носят характера доказательства, а лишь косвенно объясняют, почему не следует ожидать сходимости при 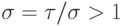 .
.
Сформулируем теперь условие Куранта - Фридрихса - Леви (условие КФЛ), необходимое для сходимости разностной задачи.
Пусть некая точка A принадлежит области определения решения u(t , x) и значение функции u(A) зависит от значения некоторой функции 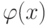 в точках x, принадлежащих множеству
в точках x, принадлежащих множеству 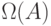 , которое, в свою очередь, принадлежит области определения функции
, которое, в свою очередь, принадлежит области определения функции 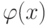 .
.
Положим, что для приближенного вычисления решения уравнения 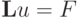 используется разностная схема
используется разностная схема 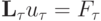 , причем, значение решения в точке Ax расчетной сетки, ближайшей к A, полностью определяются значениями функции
, причем, значение решения в точке Ax расчетной сетки, ближайшей к A, полностью определяются значениями функции 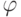 на множестве
на множестве 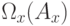 . Для того чтобы имела место сходимость
. Для того чтобы имела место сходимость 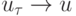 при
при  , разностная схема должна быть устроена так, чтобы при сколь угодно малых значениях пространственного шага h в произвольной окрестности любой точки области
, разностная схема должна быть устроена так, чтобы при сколь угодно малых значениях пространственного шага h в произвольной окрестности любой точки области 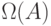 имелась точка множества
имелась точка множества 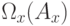 .
.
Другими словами, разностная схема должна быть устроена так, чтобы область зависимости разностного уравнения учитывала область зависимости решения исходного дифференциального уравнения. В противном случае сходимости ожидать, вообще говоря, нельзя. Если же разностная задача аппроксимирует дифференциальную, то необходимое условие сходимости КФЛ является также необходимым условием устойчивости схемы. Отметим, что условию КФЛ можно придать форму теоремы.