Численные методы решения уравнений в частных производных

:

Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Уровень: профессионал | Доступ: платный

Лекция 5: Численное решение уравнений в частных производных гиперболического типа с большими градиентами решений

A
|
версия для печати
< Лекция 4 || Лекция 5: 123456789 || Лекция 6 >
Аннотация: Лекция продолжает тему предыдущей лекции и также является необязательной. В ней рассматриваются некоторые идеи, нашедшие свое применение для построения разностных схем решения задач механики сплошной среды. Рассматриваются способы построения гибридных схем для задач с большими градиентами решения, описываются идеи TVD - и ENO - схем. Вкратце описываются разностные схемы, построенные на основе решения задачи о распаде произвольного газодинамического разрыва (схемы С.К. Годунова)
Ключевые слова: запись, потоковая форма представления разностных схем, выражение, представление, параметр, переключатель, гибридные схемы, точность, шаблон, пространство неопределенных коэффициентов, однородное уравнение, определение, уравнениями в частных производных, матрица, вектор, матрица перехода, базис, собственный вектор, векторные, уравнения газовой динамики, погрешность, поток, диффузия, антидиффузия, коэффициенты, TVD - схемы, функция, вариация, численное решение уравнений, константы, ENO - схемы, искусственная вязкость, линейное уравнение переноса, невязка, ПДП, вторая производная, объединение, дивергентная форма, квазилинейное уравнение переноса, scheme, величина потока, неявная разностная схема, множитель, подстановка, алгоритм, коррекция, метод С.К.Годунова, матричная форма, контур, равенство, Произведение, системы нелинейных уравнений, устойчивость

5.1. Потоковая форма представления разностных схем

Рассмотрим линейное одномерное уравнение переноса

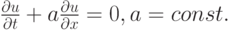
$ \frac{{\partial}u}{{\partial}t} + a \frac{{\partial}u}{{\partial}x} = 0, a = {const} . $

Приблизим его при помощи схем "левый уголок" и "правый уголок" в зависимости от направления переноса (схемы Куранта - Изаксона - Риса [15.1] или С.К.Годунова [15.2]):

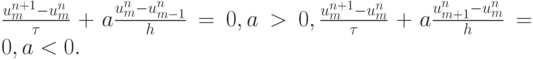
$ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + a \frac{{u_m^{n} - u_{m - 1}^{n}}}{h} = 0, a > 0, \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + a \frac{{u_{m + 1}^{n} - u_m^{n}}}{h} = 0, a < 0. $

Можно объединить форму записи приведенных выше выражений и записать схему как

$ u_m^{n + 1} = u_m^{n} - \sigma \left\{ \begin{array}{cc} {u_{m + 1}^{n} - u_m^{n}, & a < 0} \\ {u_m^{n} - u_{m - 1}^{n}, & a \ge 0} \\ \end{array} \right. {\sigma}= a \frac{\tau}{h} \mbox{ - число Куранта.} $

Введя обозначения

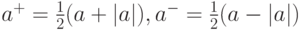
$ a^{+} = \frac{1}{2}(a + \left| a\right|), a^{-} = \frac{1}{2}(a - \left| a\right|) $
, приведенную выше объединенную запись можно представить еще в двух формах:

$ u_m^{n + 1} = u_m^{n} - \frac{\tau}{h}(a^{-}(u_{m + 1}^{n} - u_m^{n} ) + a^{+}(u_m^{n} - u_{m - 1}^{n} )), $

или

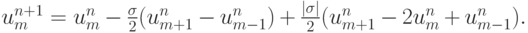
$ u_m^{n + 1} = u_m^{n} - \frac{{\sigma}}{2}(u_{m + 1}^{n} - u_{m - 1}^{n} ) + \frac{{\left| \sigma\right|}}{2}(u_{m + 1}^{n} - 2u_m^{n} + u_{m - 1}^{n} ). $

Представим разностную схему в потоковом виде, для чего введем функции 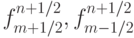f_{m + 1/2}^{n + 1/2}, f_{m - 1/2}^{n + 1/2} так, что данные на следующем слое по времени можно представить в виде

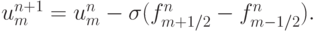
u_m^{n + 1} = u_m^{n} - \sigma (f_{m + 1/2}^{n} - f_{m - 1/2}^{n} ).

Тогда простое сравнение выражений даст возможность записать потоки, для них легко получаются выражения

\begin{gather*}f_{m + 1/2}^{n} = \frac{1}{2}((u_{m + 1}^{n} + u_m^{n} ) - \sign a(u_{m + 1}^{n} - u_m^{n} )), \\ f_{m - 1/2}^{n} = \frac{1}{2}((u_m^{n} + u_{m - 1}^{n} ) - \sign a(u_m^{n} - u_{m - 1}^{n} )). \end{gather*}

В [15.3] приведен общий вид неявной схемы, записанной в потоковом виде

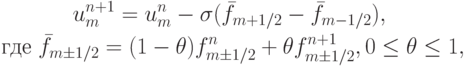
\begin{gather*} u_m^{n + 1} = u_m^{n} - \sigma (\bar{f}_{m + 1/2} - \bar{f}_{m - 1/2} ), \\ \mbox{ где } \bar{f}_{m \pm 1/2} = (1 - \theta )f_{m \pm 1/2}^{n} + \theta f_{m \pm 1/2}^{n + 1}, 0 \le \theta \le 1, \end{gather*}

выражение для 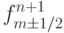f_{m \pm 1/2}^{n + 1} аналогично выражению для f_{m \pm 1/2}^{n}.

Введем также двухпараметрическое семейство разностных схем [15.4]

$ u_m^{n + 1} = u_m^{n} + a \frac{\tau}{h}(\bar{f}_{m + 1/2}^{n} - \bar{f}_{m - 1/2}^{n} ), $

в которых потоки будут определяться в зависимости от направления переноса A. Они также будут зависеть от значений параметров:

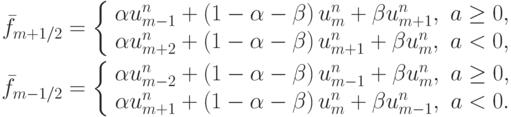
\begin{gather*} \bar{f}_{m + 1/2} = \left\{ \begin{array}{cc} {\alpha u_{m - 1}^{n} + \left({1 -{\alpha} -{\beta}}\right) u_m^{n} +{\beta}u_{m + 1}^{n}, & a \ge 0, } \\ {\alpha {u}_{m + 2}^{n} + \left({1 -{\alpha} -{\beta}}\right) u_{m + 1}^{n} + {\beta}u_m^{n}, & a < 0, } \end{array} \right. \\ \bar{f}_{m - 1/2} = \left\{ \begin{array}{cc} {\alpha u_{m - 2}^{n} + \left({1 -{\alpha} -{\beta}}\right) u_{m - 1}^{n} +{\beta}u_m^{n}, & a \ge 0, } \\ {\alpha u_{m + 1}^{n} + \left({1 -{\alpha} -{\beta}}\right) u_m^{n} +{\beta}u_{m - 1}^{n}, & a < 0.} \\ \end{array} \right. \end{gather*}

5.2. Гибридные схемы

Для построения первой гибридной разностной схемы в работе [15.5] использовалось следующее представление ( a > 0 ):

$ u_m^{n + 1} = u_m^{n} - \frac{{{\tau}a}}{h}(u_m^{n} - u_{m - 1}^{n} ) + \frac{\gamma }{2} \frac{{a{\tau}}}{h} \left({1 - \frac{{a{\tau}}}{h}}\right)(u_{{m} + 1}^{n} - 2u_m^{n} + u_{m - 1}^{n} ) = 0, $

где \gamma — параметр гибридности. От него зависит порядок разностной схемы, по которой будет производиться расчет в областях с большими локальными градиентами решения. В цитируемой работе [15.5]

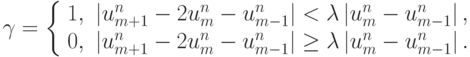$ {\gamma = \left\{ \begin{array}{cc} {{1}, & \left| {u_{{m} + 1}^{n} - 2u_m^{n} - u_{m - 1}^{n}}\right| < \lambda \left| {u_m^{n} - u_{m - 1}^{n}}\right|, } \\ {{0}, & \left| {u_{{m} + 1}^{n} - 2u_m^{n} - u_{m - 1}^{n}}\right| \ge \lambda \left| {u_m^{n} - u_{m - 1}^{n}}\right|.} \\ \end{array} \right. ( 5.1)

При \lambda = 0 схема имеет первый порядок точности, при сколь угодно больших \lambda — второй. Можно повысить порядок аппроксимации этой схемы до третьего:

\begin{gather*} u_m^{n + 1} = u_m^{n} - \frac{{\tau}a}{h}(u_m^{n} - u_{m - 1}^{n} ) + \\ + \frac{\gamma }{2} \frac{{a{\tau}}}{h} \left({1 - \frac{{a{\tau}}}{h}}\right) \left\{{(u_{{m} + 1}^{n} - 2u_m^{n} + u_{m - 1}^{n} ) + (u_{{m} + 1}^{n} - 3u_m^{n} + 3u_{m - 1}^{n} - u_{{m} - 2}^{n} )}\right\} . \end{gather*}

В [15.21] схему, записанную в потоковой форме представления, предложено сделать гибридной, вводя потоки:

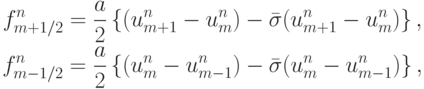
\begin{gather*} f_{{m} + 1/2}^{n} = \frac{a}{2} \left\{{(u_{{m} + 1}^{n} - u_m^{n} ) - \bar{\sigma} (u_{{m} + 1}^{n} - u_m^{n} )}\right\}, \\ f_{{m} - 1/2}^{n} = \frac{a}{2} \left\{{(u_m^{n} - u_{m - 1}^{n} ) - \bar{\sigma} (u_m^{n} - u_{m - 1}^{n} )}\right\}, \end{gather*}

при такой записи

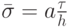
$ \bar{\sigma} = a \frac{\tau}{h} $
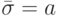в области гладкого решения и \bar{\sigma} = \sign a в области с большими градиентами решения. Переключатель между "гладким" и "негладким" решениями может быть построен аналогично (5.1). Другие способы построения переключателей описаны в [15.6], [15.7]. В [15.6] построены сеточно - характеристические гибридные схемы.

Дальше >>
< Лекция 4 || Лекция 5: 123456789 || Лекция 6 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 29
Максим Радунцев
Максим Радунцев
Россия
предложить дружбу
Надежда Павленко
Надежда Павленко
Россия, Ставрополь
предложить дружбу