Численные методы решения уравнений в частных производных

:

Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Уровень: профессионал | Доступ: платный
Лекция 6:

Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона
A
|
версия для печати
< Лекция 5 || Лекция 6: 123456789101112 || Лекция 7 >
Аннотация: В лекции разбираются постановка простейшей разностной задачи для уравнений Лапласа и Пуассона в прямоугольной области (схема "крест"). Дается обзор методов решения сеточных уравнений. Вкратце описываются идеи современных методов решения эллиптических уравнений в области произвольной геометрии — многосеточный метод и метод построения мажорантных разностных схем в пространстве неопределенных коэффициентов
Ключевые слова: методы решения сеточных уравнений, размерность, итерационные методы, функция, запись, шаблон, схема крест, производные, разложение в ряд, выражение, невязка, устойчивость, значение, доказательство, объединение, разрешимость, норма, максимум, разностный принцип максимума, система линейных уравнений, полином, погрешность, радиус, индекс, проекция, неравенство, решение системы линейных уравнений, разреженные матрицы, матрица, матрица обратная, Метод простых итераций, операторы перехода, метод Фурье, число обусловленности матрицы, метод итерации, трехслойный итерационный метод, численное решение уравнений, метод переменных направлений, уравнениями в частных производных, собственный вектор, коэффициенты Фурье, чебышевский набор параметров, методы Якоби, Зейделя, верхней релаксации, попеременно - треугольный итерационный метод, параметр, действительное число, константы, нижней треугольной, алгоритм, анализ, равенство, конечный ряд Фурье, коэффициенты, компонент, многосеточный метод Р.П.Федоренко, интерполяция, вычисление, мажорантные разностные схемы, метод Гаусса, итерационный алгоритм

Среди всех типов уравнений математической физики эллиптические уравнения с точки зрения вычислителей стоят особняком. С одной стороны, имеется хорошо развитая теория решения эллиптических уравнений и систем. Достаточно легко доказываются теоремы об устойчивости разностных схем для эллиптических уравнений. Во многих случаях получаются априорные оценки точности расчетов и числа итераций при решении возникающих систем сеточных уравнений. С другой стороны, системы сеточных уравнений, возникающие при решении уравнений методами сеток, имеют большую размерность и плохо обусловлены. Для решения таких систем разработаны специальные итерационные методы.

6.1. Постановка задачи. Простейшая разностная схема "крест". Устойчивость схемы "крест"

Будем рассматривать двухмерное уравнение Пуассона

$ \frac{{\partial}^2 u}{{\partial}x^2} + \frac{{\partial}^2 u}{{\partial}y^2} = f(x, y) $

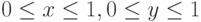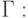
в единичном квадрате 0 \le x \le 1, 0 \le y \le 1 с краевыми условиями первого рода на границе расчетной области \Gamma:

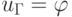
u_{\Gamma} = \varphi

( \varphi — заданная на границе функция).

В случае прямоугольной области граничные условия удобно записать в следующем виде:

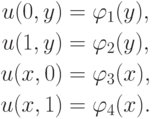
\begin{gather*} u(0, y) = \varphi_1 (y), \\ u(1, y) = \varphi_2 (y), \\ u(x, 0) = \varphi_3 (x), \\ u(x, 1) = \varphi_4 (x). \end{gather*}

Для простоты выкладок введем равномерную расчетную сетку с узлами {xm, yl}, m, l = 0, 1, ... , M с равным количеством шагов по каждому пространственному направлению, сеточную область D — совокупность всех узлов сетки, включая граничные, и сеточную функцию { uml }. В этом случае шаги по координатам предполагаются равными. В случае неравных шагов по каждому направлению полученные результаты не изменятся, а запись уравнений станет более громоздкой.


Выбираем простейший пятиточечный шаблон разностной схемы "крест". На этом шаблоне аппроксимирующее разностное уравнение легко выписать. Для этого производные заменим вторыми разностями:

$ \frac{{u_{m - 1, l} - 2u_{ml} + u_{m + 1, l}}}{{h^2}} + \frac{{u_{m, l - 1} - 2u_{ml} + u_{m, l + 1}}}{{h^2}} = f_{ml}, $

где h — шаг по координатам, или в операторной форме

{\mathbf{\Lambda}}_1 u_{ml} + {\mathbf{\Lambda}}_2 u_{ml} = f_{ml},

здесь

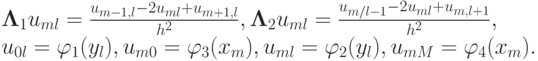
${{\bf \Lambda }}_1 u_{ml} = \frac{{u_{{m} - 1,l} - 2u_{ml} + u_{{m} + 1,l} }}{{h^2 }}, {{\bf \Lambda }}_2 u_{ml} = \frac{{u_{{m}/l - 1} - 2u_{ml} + u_{{m},l + 1} }}{{h^2 }},$\\ $u_{0l} = \varphi _1 (y_l ), u_{{m}0} = \varphi _3 (x_{m} ), u_{ml} = \varphi _2 (y_l ), u_{{m}{M}} = \varphi _4 (x_{m} ). $

Эту же разностную схему можно записать в каноническом виде для разностных схем для эллиптических уравнений:

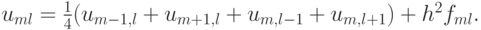
$ u_{ml} = \frac{1}{4}(u_{{m} - 1, l} + u_{{m} + 1, l} + u_{{m}, l - 1} + u_{{m}, l + 1}) + h^2 f_{{m}l}. $

Такую каноническую запись не следует путать с канонической формой записи итерационного метода, которая встретится ниже.

Такая схема обладает вторым порядком аппроксимации по обеим координатам. Это легко показать, применяя разложение в ряд Тейлора функции — проекции точного решения на сетку — вплоть до членов четвертого порядка включительно. Проведем такое разложение для одного из операторов, стоящих в данном разностном уравнении:

$ {\mathbf{\Lambda}}_1 u_m = \frac{{u_{m - 1} - 2u_m + u_{{m} + 1}}}{{h^2}} = \left({\frac{{{\partial}^2 u}}{{{\partial}x^2}}}\right)_m + \frac{{h^2}}{{12}} \left({\frac{{{\partial}^4 u}}{{\partial u^4 }}}\right)_m + O(h^4 ). $

Здесь учтено разложение проекции точного решения в ряд Тейлора

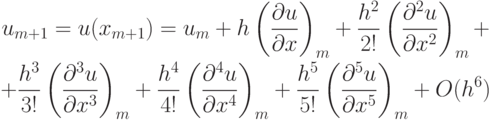
\begin{gather*} u_{{m} + 1} = u(x_{{m} + 1}) = u_m + h \left({\frac{{\partial}u}{{\partial}x}}\right)_m + \frac{{h^2}}{{2!}} \left({\frac{{{\partial}^2 u}}{{{\partial}x^2}}}\right)_m + \\ + \frac{{h^3 }}{{3!}} \left({\frac{{{\partial}^3 u}}{{{\partial}x^3 }}}\right)_m + \frac{{h^4 }}{{4!}} \left({\frac{{{\partial}^4 u}}{{{\partial}x^4 }}}\right)_m + \frac{{h^5 }}{{5!}} \left({\frac{{{\partial}^5 u}}{{{\partial}x^5 }}}\right)_m + O(h^6 ) \end{gather*}

и аналогичное разложение для um - 1.

Для рассматриваемого двухмерного уравнения получим выражение для главного члена невязки

$ {\mathbf{\Lambda}}_1 u_{ml} + {\mathbf{\Lambda}}_2 u_{ml} = \left[{\frac{{\partial}^2 u}{{\partial}x^2} + \frac{{\partial}^2 u} {{\partial}y^2}}\right]_{ml} + \frac{h^2}{12} \left[{\frac{{\partial}^4 u} {{\partial}x^4} + \frac{{\partial}^4 u}{{\partial}y^4 }}\right]_{ml} + O(h^4 ). $

Рассмотрим устойчивость полученной схемы. Отметим, что методы исследования на устойчивость, применяемые для эволюционных (зависящих от времени) уравнений, здесь не работают. Действовать приходится на основе определения устойчивости.

Сформулируем и докажем две леммы, которые облегчат процедуру доказательства устойчивости разностной схемы.

Дальше >>
< Лекция 5 || Лекция 6: 123456789101112 || Лекция 7 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 30
Максим Радунцев
Максим Радунцев
Россия
предложить дружбу
Надежда Павленко
Надежда Павленко
Россия, Ставрополь
предложить дружбу