| Россия |
Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона
6.4. Сводка результатов по итерационным методам решения сеточных уравнений
После рассмотрения самых распространенных методов решения сеточных уравнений получена возможность сравнить итерационные методы по количеству итераций, необходимых для достижения точности 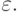 Приведем только выражения для сомножителя, пропорционального числу узлов сетки.
Приведем только выражения для сомножителя, пропорционального числу узлов сетки.





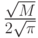

 .
.6.5. Основные идеи многосеточного метода Р.П.Федоренко
Вернемся к рассмотренному выше вопросу о сходимости итерационных методов решения систем сеточных уравнений, получающихся при решении уравнений Лапласа или Пуассона. Выше был проведен спектральный анализ итерационных методов решения такой системы. Вернемся, например, к результатам исследования метода переменных направлений. Для него установлено равенство для коэффициентов разложения в конечный ряд Фурье невязки

Из этого выражения следует, что коэффициенты при высокочастотных составляющих (т.е. при достаточно больших  при фиксированном
при фиксированном  ) убывают достаточно быстро, в то время как при низкочастотных гармониках (
) убывают достаточно быстро, в то время как при низкочастотных гармониках ( 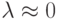 ) коэффициенты убывают медленно. Такой же эффект существует и для других итерационных методов.
) коэффициенты убывают медленно. Такой же эффект существует и для других итерационных методов.
Рассмотрим сеточное уравнение Пуассона
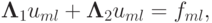 |
( 6.1) |
и, кроме того, уравнение
 |
( 6.2) |
где r — невязка, e — погрешность решения. Если известно приближенное решение задачи (6.1), то, решая (6.2), можно найти решение исходной системы по формуле

но решение задачи (6.2) по сложности точно такое же, как и решение исходной задачи.
Если применять итерационный метод (6.1), сделав несколько итераций, то приближенное решение задачи будет известно, а невязка станет плавно меняющейся функцией — в разложении в конечный ряд Фурье будут отсутствовать высокочастотные составляющие. Невязка будет хорошо представляться на более грубой сетке, тогда размерность вспомогательной системы (6.2) понизится.
Введем сетку с шагом 2h и рассмотрим на ней задачу (6.2). Размерность системы сеточных уравнений получилась в четыре раза меньше, чем размерность исходной системы. Предположим, что есть средство эффективно решать такие задачи. После этого для восстановления решения надо найти невязку на более подробной сетке. Строим оператор интерполяции с грубой сетки на подробную. Очевидно, что ошибка интерполяции будет иметь высокочастотный компонент. Тогда используем полученное решение (низкочастотные компоненты погрешности погашены на грубой сетке, остались только высокие частоты) в качестве начального приближения и делаем несколько сглаживающих итераций. Этот этап называется коррекцией с грубой сетки.
Схема приближенного построения решения получается следующей.
- Решается уравнение (6.) на подробной сетке, проводится несколько сглаживающих итераций,
- По приближенному решению находится невязка
 ,
, - Ищется ограничение (проекция) невязки на грубую сетку.
- На грубой сетке решается уравнение
 .
. - Строится оператор интерполяции решения на подробную сетку, значения невязки пересчитываются на подробную сетку.
- На подробной сетке проводится несколько сглаживающих итераций для уравнения
 .
. - Ищется решение по формуле
 .
.
Выполнение пункта 4 — решения сеточной системы — может оказаться трудоемким, поэтому внутри этого шага алгоритма можно еще раз перейти к более грубой сетке. Многосеточный метод состоит в рекурсивном повторении данной процедуры до тех пор, пока не будет получена система малой размерности, которая может быть эффективно решена прямым методом (например, Гаусса или сопряженных градиентов).
Простейшая реализация многосеточного метода — каскадный алгоритм. Он предусматривает последовательное решение задач на сетке со все большим числом узлов, а интерполяция решения с более грубой сетки используется в качестве начального приближения. Для самосопряженных эллиптических задач часто используется V - цикл. Сначала ищется решение на подробной сетке, затем проводится последовательно вычисление невязок на все более грубых сетках, затем — несколько коррекций с грубой сетки и сглаживающие итерации на все более и более подробных сетках. Для несамосопряженных задач лучше зарекомендовал себя W - цикл, когда сначала вспомогательная система решается на последовательности все более и более грубых сеток, затем идут итерации на все более подробных сетках, затем снова итерации на грубых сетках и затем — на подробных вплоть до сетки с максимальным числом разбиений.
Впервые многосеточный метод предложен в [16.10]. Более подробно о многосеточных методах и реализации многосеточных алгоритмов можно прочитать в [16.8] и статьях Н.С.Бахвалова с соавторами и Ю.В.Василевского с соавторами в [16.9].
