| Россия |
Лекция 2: Численное решение дифференциальных уравнений в частных производных параболического типа на примере уравнения теплопроводности
2.1. Постановки задач для уравнений параболического типа
Рассмотрим численные методы решения уравнений параболического типа.
Одномерное линейное уравнение теплопроводности (диффузии). Напомним постановку соответствующей смешанной задачи:
![$
{\frac{{\partial}u}{{\partial}t} = a \frac{{\partial}^2 u}{{\partial}x^2} + f(t, x), t \in [0, T], x \in [0, X].} $](/sites/default/files/tex_cache/14f9bf47c108cfc6dd8b51390112ac48.png) |
( 2.1) |
Здесь a = a(x, t) > 0. Для того чтобы задача была поставлена корректно, необходимо задать начальное условие
u(0, x) = u0(x), t = 0,
и граничные условия

О свойствах решений линейного уравнения теплопроводности подробнее в [12.1], [12.3].
Одномерное квазилинейное уравнение теплопроводности (диффузии):
![$
{\frac{{\partial}u}{{\partial}t} = \frac{{\partial}}{{\partial}x} \left[{a(u) \frac{{\partial}u}{{\partial}x}\right] + f(u), \quad t \in \left[{0, {\rm T}}\right], x \in \left[{0, X}\right].} $](/sites/default/files/tex_cache/320f87db4232f415ecf9c2039fd82a89.png) |
( 2.2) |
Уравнения такого вида встречаются в теории горения, астрофизике, физике плазмы, теории сверхпроводимости Гинзбурга - Ландау, динамике популяций и других приложениях. Здесь a(u) > 0 при любых значениях u, кроме того,  . Для глобальной ограниченности решения также требуется выполнение условия
. Для глобальной ограниченности решения также требуется выполнение условия

Двухмерное линейное уравнение теплопроводности (диффузии):
![$ {\frac{{\partial}u}{{\partial}t} = \frac{{{\partial}^2 u}}{{{\partial}x^2}} + \frac{{{\partial}^2 u}}{{{\partial}y^2}}, t \in \left[{0, {\rm T}}\right], x \in \left[{0, X}\right], y \in \left[{0, Y}\right].} $](/sites/default/files/tex_cache/d7184ab21ce1f90f21a2b1e2c9aee7c8.png) |
( 2.3) |
Для численного решения уравнения (2.1), по - видимому, наиболее известной является параметрическая двухслойная шеститочечная разностная схема вида
![{\frac{{u_m^{n + 1} - u_m^{n}}}{\tau} = a \left[{\xi \frac{{u_{m - 1}^{n + 1} - 2u_m^{n + 1} + u_{m + 1}^{n + 1}}}{h^2} + (1 - \xi ) \frac{{u_{m - 1}^{n} - 2u_m^{n} + u_{m + 1}^{n}}}{h^2}}\right], }](/sites/default/files/tex_cache/c4c50a8201f58fd3867dc366462573ff.png) |
( 2.4) |
где ![\xi \in \left[{0, 1}\right]](/sites/default/files/tex_cache/090c31ad392dcbc50d54ca761a846e98.png) .
.
При  имеем явную схему
имеем явную схему


 .
.При  имеем неявную схему
имеем неявную схему

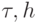 , с порядком аппроксимации
, с порядком аппроксимации  .
.При  разностный метод называется схемой Кранка - Никольсон:
разностный метод называется схемой Кранка - Никольсон:

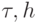 и имеет порядок аппроксимации
и имеет порядок аппроксимации  . Эта схема, в отличие от двух предыдущих, не является монотонной, т.е. она может давать осцилляции разностного происхождения на решениях, имеющих большие градиенты.
. Эта схема, в отличие от двух предыдущих, не является монотонной, т.е. она может давать осцилляции разностного происхождения на решениях, имеющих большие градиенты.Схема, имеющая второй порядок точности по  и четвертый по h, получается на расширенном шаблоне с учетом разностной
аппроксимации главного члена невязки. При исследовании аппроксимации явной двухслойной схемы получим
и четвертый по h, получается на расширенном шаблоне с учетом разностной
аппроксимации главного члена невязки. При исследовании аппроксимации явной двухслойной схемы получим

