НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 2: Численное решение дифференциальных уравнений в частных производных параболического типа на примере уравнения теплопроводности

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: профессионал | Доступ: платный

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать программу

2.5. Задачи

Исследовать на аппроксимацию и устойчивость схему Ричардсона
$\frac{{u_m^{n + 1} - u_m^{n - 1}}}{{2{\tau}}} = \frac{a}{h^2}{\mathbf{\Lambda}}_{xx} u^{n},$
с шаблоном

Рис. 2.6.

аппроксимирующую уравнение теплопроводности
$\frac{{\partial}u}{{\partial}t} = a \frac{{{\partial}^2 u}}{{{\partial}x^2}}.$

Решение. В силу симметрии шаблона схемы несложно заметить, что ее порядок аппроксимации $O(\tau ^{2}, h^{2})$ .

Подстановка решения в виде $u_m^{n} = {\lambda}^{n}e^{i{\alpha} m}$ дает квадратное уравнение для определения спектра оператора послойного перехода
${\lambda}^2 + \frac{{8a{\tau}}}{{h^2}} {\lambda}{\sin}^2 \frac{{\alpha h}}{2} - 1 = 0,$
один из корней которого при любом значении параметра ${\alpha}$ по модулю больше единицы, т. е. рассматриваемая схема безусловно неустойчива.

Выходом из данной ситуации оказывается замена в выражении
${{\Lambda}}_{xx} u_m^{n} = \frac{{u_{m - 1}^{n} - 2u_m^{n} + u_{m + 1}^{n}}}{{h^2}}$
величины $u_m^{n}$ на
$\frac{{u^{n - 1} + u^{n + 1}}}{2}$
(схема Франкела - Дюффорта):

$\frac{{u_m^{n + 1} - u_m^{n - 1}}}{{2{\tau}}} = \frac{a}{h^2} \left[{u_{m - 1}^{n} - \left({u_m^{n + 1} + u_m^{n - 1}}\right) + u_{m + 1}^{n}}\right]$

со следующим шаблоном:

Рис. 2.7.

которая разрешается явно относительно 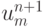$u_m^{n + 1}$ и безусловно устойчива.

Однако она обладает лишь условной аппроксимацией: $O(\tau ^{2}, h^{2}, \tau ^{2}/h^{2})$ , и таким образом, сходимость возможна лишь при ${\tau}/h \to 0$ .
Исследовать на аппроксимацию и устойчивость схему Саульева бегущего счета
$\frac{{u_m^{n} - u_m^{n - 1}}}{\tau} = a \frac{{u_{m - 1}^{n} - (u_m^{n} + u_m^{n - 1} ) - u_{m + 1}^{n - 1}}}{h^2}$

(четные слои, счет справа налево)

$\frac{{u_m^{n + 1} - u_m^{n}}}{\tau} = a \frac{{u_{m - 1}^{n} - (u_m^{n} + u_m^{n + 1} ) + u_{m + 1}^{n + 1}}}{h^2}$

(нечетные слои, счет слева направо) со следующим шаблоном:

Рис. 2.8.

Решение. Путем подстановки решения в виде $u_m^{n} = {\lambda}^{n} e^{i{\alpha} m}$ , несложно проверить, что схема безусловно устойчива.

Невязка каждого из двух уравнений, вычисленная относительно точек, отмеченных крестиками, имеет порядок $O(\tau ^{2}, h^{2}, \tau , h, \tau /h)$ .

Сложение же невязок из двух рассматриваемых уравнений дает погрешность $O(\tau ^{2}, h^{2}, \tau ^{2}/h^{2})$ , аналогичную схеме Франкела - Дюфорта.

Схема Саульева допускает значительное улучшение. Достаточно только вычислить значения функции в рамках перехода с данного слоя на следующий два раза — бегущим счетом слева направо и бегущим счетом справа налево — и усреднить результаты. Свойства такого метода расчета предлагается исследовать самостоятельно.
Исследовать на аппроксимацию и устойчивость схему Алена - Чена
$\frac{{u_m^{n + 1} - u_m^{n}}}{\tau} = a \frac{{u_{m - 1}^{n} - 2u_m^{n + 1} + u_{m + 1}^{n}}}{{h^2}}$

с шаблоном

Рис. 2.9.

Ответ. Во - первых, несмотря на то, что в правую часть входит значение функции 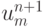$u_m^{n + 1}$ , вычисляемое на верхнем слое, разностное уравнение разрешается относительно 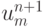$u_m^{n + 1}$ . Схема безусловно устойчива, что является ее достоинством при реализации, однако она имеет порядок аппроксимации $O(\tau , h^{2}, \tau /h^{2})$ , т.е. схема является условно аппроксимирующей.
Выяснить, является ли явная четырехточечная схема
$\frac{{u_m^{n + 1} - u_m^{n}}}{\tau} = a{{{\Lambda}}}_{xx}{u}^{n}$
с шаблоном

Рис. 2.10.

монотонной. Монотонные разностные схемы (по Фридрихсу) — это схемы, которые при записи в виде, разрешенном относительно 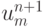$u_m^{n + 1}$ при значениях сеточной функции во всех остальных точках шаблона, имеют неотрицательные коэффициенты. Монотонные разностные схемы не дают паразитные осцилляции в решении. Придумать доказательство утверждения, что из монотонности разностной схемы следует ее устойчивость, предлагается самостоятельно.

Решение. Представим рассматриваемую схему в виде

$u_m^{n + 1} = \sum\limits_{k = - 1}^1 {\alpha_m u_{m + k}}$
где
${\alpha} = 1 - \frac{2a{\tau}}{h^2},{\alpha}_1 ={\alpha}_{- 1} = \frac{a{\tau}}{h^2},$
откуда видно, что схема является монотонной при выполнении условия ${\alpha}_k \ge 0, k = - 1, 0, 1$ то есть при
${\tau}\le \frac{h^2}{2a}$
. Эта схема условно монотонная.

Заметим, что неявная четырехточечная схема является монотонной, а схема Кранка - Никольсон — условно монотонная.

Рис. 2.11.

Исследование монотонности параметрической двуслойной схемы в виде $u_m^{n + 1} = \sum\limits_{k = 0}^ \infty {\alpha_m u_{m + k}}$ , дает (выкладки опускаем ввиду их громоздкости):

$\begin{gather*} u_m^{n + 1} ={\alpha}_0 u_m + \sum\limits_{k = 1}^ \infty {\alpha_k (u_{m - k} + u_{m + k} )}, \\ {\alpha}_0 = 1 - \frac{{4a{\tau}\left({h + \sqrt {h^2 + 4 \xi a{\tau}}}\right)^{- 1}}}{{\sqrt {h^2 + 4 \xi a{\tau}}}}, \\ {\alpha}_1 = \frac{{4a{\tau}}}{{\sqrt {h^2 + 4 \xi a{\tau}}}} \left({h + \sqrt {h^2 + 4 \xi a{\tau}}}\right)^{- 2}, \\ {\alpha}_k ={\alpha}_{k - 1} \cdot 4 \xi a{\tau}\left({h + \sqrt {h^2 + 4 \xi a{\tau}}}\right)^{- 2}, k \ge 2. \end{gather*}$

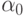Коэффициенты ${\alpha}_x$ при ${x} \ge 1$ неотрицательны, коэффициент ${\alpha}_0$ неотрицателен при выполнении условия:

${\tau}\le \frac{{\left({2 - \xi }\right)h^2}}{{4a \left({1 - \xi } \right)^2}}.$

Отсюда видно, что, за исключением неявной четырехточечной схемы с $\xi = 1$ , все неявные схемы являются монотонными лишь при условии $\tau \sim h^{2}$ .
Исследовать на устойчивость и аппроксимацию трехслойную схему
$\frac{{1, 5(u_m^{n + 1} - u_m^{n})}}{\tau} + \frac{{0, 5(u_m^{n} - u_m^{{n} - 1} )}}{h} = {\mathbf{\Lambda}}_{xx} u_m^{n + 1}$

с шаблоном

Рис. 2.12.

Ответ. Простое исследование на аппроксимацию данной схемы путем разложения функций в ряд Тейлора дает $O(\tau ^{2}, h^{2})$ . Схема безусловно устойчива. Кроме того, схема монотонна.
Показать, что решение задачи
$\begin{gather*} \frac{{\partial} u}{{\partial} t} = \frac{\partial}{{\partial} x}au^{\alpha} \frac{{\partial} u}{{\partial} x}, (\alpha > 0), \\ u \left({+ \infty , t}\right) = 0, \quad u \left({0, t}\right) = ct^{1/{\alpha} }, \quad u \left({x, 0}\right) = 0 \end{gather*}$ ( 2.5)

представляет собой бегущую волну, распространяющуюся с конечной скоростью, причем при ${\alpha} \ge 0$ на фронте волны решение терпит разрыв первой производной (т.е. является обобщенным решением).

Предложить какие - нибудь разностные схемы для численного решения данной задачи, например, применив интегро - интерполяционный метод [12.3]. Почему в этом случае нельзя переписать уравнение в виде

$\frac{{{\partial} u}}{{{\partial} t}} = au^{\alpha} \frac{{{\partial}^2 u}}{{{\partial} x^2}} + a{\alpha} u^{\alpha - 1} \left({\frac{{{\partial} u}}{{{\partial} x}}}\right)^2 ,$

продифференцировав правую часть по x, а затем заменить производные их разностными аппроксимациями?

Решение. Построим решение задачи в переменных бегущей волны:

${u = u(\xi ) = u(x - {vt}), (x - vt \ge 0), u \equiv 0.}$ ( 2.6)

Подставив (2.6) в исходное уравнение, получим следующее обыкновенное дифференциальное уравнение:

$- vu^{\prime}_\xi = a(u^{\alpha} u^{\prime}_\xi )^\prime_\xi .$ ( 2.7)

Это уравнение интегрируется по $\xi:$

$k - vu = au^{\alpha} u^{\prime}_\xi ,$ ( 2.8)

где k — константа интегрирования.

Выражение, стоящее в правой части (2.8), есть поток величины u, а уравнение (2.8) является некоторым законом сохранения. В точке фронта u = 0, в силу непрерывности потока справа и слева от фронта (2.8) должно выполняться, отсюда следует k = 0.

Так как интересуют только нетривиальные решения (2.5), то $u \ne 0$ , и можно разделить правую и левую части на u. Тогда получим

${- v = au^{\alpha - 1} u^{\prime}_\xi = \frac{a}{\alpha }(u^{\alpha} )^\prime_\xi , }$ ( 2.9)

откуда
$u = \left[{\frac{{\alpha v}}{a}(x - vt)}\right]^{1/{\alpha}}$
.

Из краевых условий при x = 0 имеем $v = ac^{\alpha}/{\alpha}$ . Наличие разрывов производной легко проверяется. Уравнение (2.5) записано в дивергентном виде, которому будет соответствовать консервативная схема.

В [12.9] использован несколько отличный подход к решению задачи.

В [12.4] рассмотрен общий случай, когда коэффициент теплопроводности есть функция K(u):

$\Phi (u) = \int\limits_{o}^{u}{\frac{{K(\eta )}}{\eta }} d \eta ; \Phi (0) = 0 ; \Phi (1) < \infty .$

Подробнее про разностные схемы для аппроксимации уравнения (5.3.1) в [12.4, c. 441 - 463].