Численные методы решения уравнений в частных производных

:

Численные методы решения уравнений в частных производных
[+]

Лекция 5: Численное решение уравнений в частных производных гиперболического типа с большими градиентами решений

A
|
версия для печати
< Лекция 4 || Лекция 5: 123456789 || Лекция 6 >

5.11. Метод С.К.Годунова

Широко распространенный метод С.К.Годунова для получения численных решений с особенностями разрывного характера основан на решении задачи о распаде разрыва [15.2, 21 - 22]. В газовой динамике хорошо известно точное решение этой задачи и рассмотрены все возможные конфигурации решений. Положим, что начальные данные есть кусочно - постоянные функции на сетке 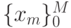\{x_m \}_0^{M}

\begin{gather*} {\mathbf{u}}(0, x) = \{{\mathbf{u}}_{m + 1/2}^0 \}, \\ {\mathbf{u}}_{m + 1/2}^{n} = {\mathbf{u}}[t_n , 0, 5(x_m + x_{m + 1} )]. \end{gather*}

Например, для системы уравнений газовой динамики 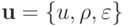{\mathbf{u}} = \{u, {\rho}, \varepsilon \}.

Иногда начальные данные задают в ячейках с целыми номерами {\mathbf{u}}(0, x) = \{{\mathbf{u}}_m^0 \}.

Решение задачи строится следующим образом. В окрестности каждого узла xm (или xm + 1/2 при другой нумерации) решается задача о распаде разрыва независимо от других возмущений. Это решение используется до того момента, когда волна, образовавшаяся от разрыва в точке xm, не встретится с волной, идущей от точки xm + 1. Далее полагаем, что и при t = t_{1} = \tau решение также приближается кусочно - постоянными функциями

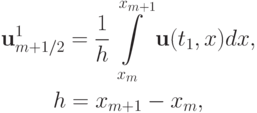
\begin{gather*} {\mathbf{u}}_{m + 1/2}^1 = \frac{1}{h} \int\limits_{x_m }^{x_{m + 1}}{{\mathbf{u}}(t_1 , x)dx}, \\ h = x_{m + 1} - x_m , \end{gather*}

или, на сетке с отличной нумерацией узлов

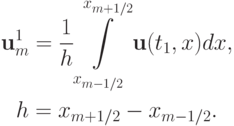
\begin{gather*} {\mathbf{u}}_m^1 = \frac{1}{h} \int\limits_{x_{m - 1/2}}^{x_{m + 1/2}}{{\mathbf{u}}(t_1 , x)dx}, \\ h = x_{m + 1/2} - x_{m - 1/2}. \end{gather*}

Представим систему дифференциальных уравнений в частных производных, записанную в дивергентном виде,

$ \frac{{\partial}{\mathbf{S}}}{{\partial}t} + \frac{{\partial}{\mathbf{P}}}{{\partial}x} = 0 $

в интегральной форме

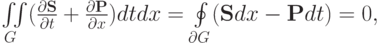
$ \iint\limits_{G} (\frac{{\partial}{\mathbf{S}}}{{\partial}t} + \frac{{\partial}{\mathbf{P}}}{{\partial}x})dtdx = \oint\limits_{{\partial}G} (\mathbf{S} dx - \mathbf{P} dt) = 0, $

где G — некая односвязная область, 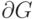\partial G — ограничивающий ее замкнутый контур, 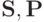\mathbf{S}, \mathbf{P} — функции от \mathbf{u}. Для этого выберем в качестве G ячейку {(tn, tn + 1) x (xm, xm + 1)} и получим интегральное уравнение

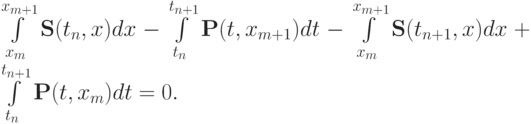
\int\limits_{x_m }^{x_{m + 1}}{{\mathbf{S}}(t_n , x)dx} - \int\limits_{t_n }^{t_{n + 1}}{{\mathbf{P}}(t, x_{m + 1} )dt} - \int\limits_{x_m }^{x_{m + 1}}{{\mathbf{S}}(t_{n + 1}, x)dx} + \int\limits_{t_n }^{t_{n + 1}}{{\mathbf{P}}(t, x_m )dt} = 0.

Первый и третий интегралы вычисляются просто по формуле средних — функции на отрезке [xm, xm + 1] кусочно - постоянны. Положив все функции кусочно - постоянными и на отрезке [tn, tn + 1] в силу автомодельности решения задачи Римана относительно переменных ( x/t ), получим равенство

{\mathbf{S}}_{m + 1/2}^{n} h - {\mathbf{P}}_{m + 1}^{n}{\tau}- {\mathbf{S}}_{m + 1/2}^{n + 1} h + {\mathbf{P}}_m^{n}{\tau} = 0,

или, разделив правую и левую части на произведение \tau h,

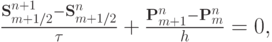
$ \frac{{{\mathbf{S}}_{m + 1/2}^{n + 1} - {\mathbf{S}}_{m + 1/2}^{n}}}{\tau} + \frac{{{\mathbf{P}}_{m + 1}^{n} - {\mathbf{P}}_m^{n}}}{h} = 0, $

или

$ \frac{{{\mathbf{S}}_m^{n + 1} - {\mathbf{S}}_m^{n}}}{\tau} + \frac{{{\mathbf{P}}_{m + 1/2}^{n} - {\mathbf{P}}_{m - 1/2}^{n}}}{h} = 0 $
при другой индексации.

При этом потоки 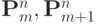\mathbf{P}_m^{n}, \mathbf{P}_{m + 1}^{n} вычисляются при помощи решения задачи о распаде разрыва, которая сводится к решению системы нелинейных уравнений.

Повышение порядка аппроксимации схем типа Годунова, основанных на решении задачи распада разрыва (или солверов Римана) реализуется путем использования кусочно - линейной аппроксимации искомых величин внутри ячеек (в отличие от кусочно - постоянного их представления в методе Годунова ) и различных алгоритмов пересчета по времени (алгоритмов типа предиктор - корректор) [15.19], [15.20].

Рассмотрим один из таких методов. Пусть внутри ячеек для всех сеточных функций заданы кусочно - линейные распределения

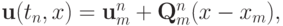
{\mathbf{u}}(t_n , x) = {\mathbf{u}}_m^{n} + {\mathbf{Q}}_m^{n} (x - x_m ),

где {\mathbf{Q}}_m^{n} — вектор наклонов функций u внутри ячейки. При этом изменение этой функции по времени внутри ячейки будет

$ \frac{{{\partial}{\mathbf{u}}}}{{\partial}t} = - {\mathbf{A}} \frac{{{\partial}{\mathbf{u}}}}{{\partial}x} = - {\mathbf{AQ}}_m^{n}. $

Предиктор (первый шаг) выглядит следующим образом:

$ \frac{\mathbf{\tilde{u}}_m - \mathbf{u}_m^n}{\tau} + \frac{\mathbf{f}(\mathbf{u}_m^n + \frac{h}{2}\mathbf{Q}_m^n) - \mathbf{f}(u_m^n - \frac{h}{2}\mathbf{Q}_m^n)}{h} = 0; $

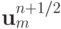{\mathbf{u}}_m^{n + 1/2} на промежуточном слое n + 1/2 вычисляем, как среднее арифметическое

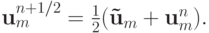
{\mathbf{u}}_m^{n + 1/2} = {{1 \over 2}}({\mathbf{\tilde{u}}}}_m + {\mathbf{u}}_m^{n} ).

На втором шаге — корректор — получим, используя метод конечных объемов

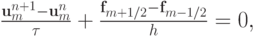
$ \frac{{{\mathbf{u}}_m^{n + 1} - {\mathbf{u}}_m^{n}}}{\tau} + \frac{{{\mathbf{f}}_{m + 1/2} - {\mathbf{f}}_{m - 1/2}}}{h} = 0, $

где, 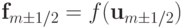{\mathbf{f}}_{m \pm 1/2} = f({\mathbf{u}}_{m \pm 1/2}), а функции {\mathbf{u}}_{m \pm 1/2} определяются из решения задачи Римана со следующими начальными данными:

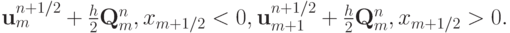
$ \mathbf{u}_m^{n + 1/2} + \frac{h}{2} \mathbf{Q}_m^{n}, x_{m + 1/2} < 0, \mathbf{u}_{m + 1}^{n + 1/2} + \frac{h}{2} \mathbf{Q}_m^{n}, x_{m + 1/2} > 0. $

Эта схемы была получена в работах [15.27], [15.29]. В качестве начальных данных можно выбирать, не изменяя порядок точности, например, такие:

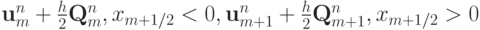
$ \mathbf{u}_m^{n} + \frac{h}{2} \mathbf{Q}_m^{n}, x_{m + 1/2} < 0, \mathbf{u}_{m + 1}^{n} + \frac{h}{2} \mathbf{Q}_{m + 1}^{n}, x_{m + 1/2} > 0 $

или 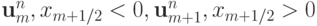\mathbf{u}_m^{n}, x_{m + 1/2} < 0, \mathbf{u}_{m + 1}^{n}, x_{m + 1/2} > 0.

Простым способом вычисления наклона Qm в ячейке с номером m для сеточной функции um, обеспечивающим устойчивость схемы, является использование функции \min\bmod (y, z) = 0, 5(sign y + sign z) \min (| y | , | z |), которая выбирает наклон с минимальным значением модуля, при условии, что знаки обоих аргументов совпадают (при разных знаках аргументов эта функция равна нулю):

$ Q_m = \min\bmod (\frac{u_{m + 1} - u_m}{h}, \frac{u_m - u_{m - 1}}{h}). $

Подобный алгоритм предиктор - корректор можно использовать и для системы уравнений, записанной в характеристической форме:

$ \frac{{{\partial}{\mathbf{u}}}}{{\partial}t} + {\mathbf{A}}({\mathbf{u}}) \frac{{{\partial}{\mathbf{u}}}}{{\partial}x} = 0, {\mathbf{A}} = {\omega }^{- 1}{{{\Lambda}\Omega }}. $

При этом предиктор имеет вид

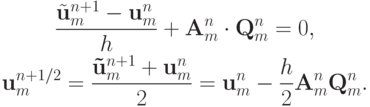
\begin{gather*} \frac{\tilde{\mathbf{u}}_m^{n + 1} - \mathbf{u}_m^n}{h} + \mathbf{A}_m^n \cdot \mathbf{Q}_m^n = 0, \\ \mathbf{u}_m^{n + 1/2} = \frac{\mathbf{\tilde{u}}_m^{n + 1} + \mathbf{u}_m^n}{2} = \mathbf{u}_m^n - \frac{h}{2}\mathbf{A}_m^n \mathbf{Q}_m^n. \end{gather*}

В качестве корректора используем, например, полученную ранее сеточно - характеристическую схему

$ \frac{{{\mathbf{u}}_m^{n + 1} - {\mathbf{u}}_m^{n}}}{\tau} + ({\omega }^{- 1}{{{\Lambda}}}^{-}{{\Omega }})_{m + 1/2}^{n} \frac{{{\mathbf{u}}_{m + 1}^{n} - {\mathbf{u}}_m^{n}}}{h} + ({\omega }^{-}{{{\Lambda}}}^{+}{{\Omega }})_{m - 1/2}^{n} \frac{{{\mathbf{u}}_m^{n} - {\mathbf{u}}_{m - 1}^{n}}}{h} = 0,

с учетом того, что начальные данные являются кусочно - постоянными:

\begin{gather*} \frac{{{\mathbf{u}}_m^{n + 1} - {\mathbf{u}}_m^{n}}}{\tau} + ({{\Omega }}^{- 1}{{{\Lambda}}}^{-}{{\Omega }})_{m + 1/2}^{n + 1/2} \frac{{{\mathbf{u}}_{m + 1}^{n + 1/2} - \frac{h}{2}{\mathbf{Q}}_{m + 1}^{n} - {\mathbf{u}}_m^{n + 1/2} - \frac{h}{2}{\mathbf{Q}}_m^{n}}}{h} + \\ + ({{\Omega }}^{- 1}{{{\Lambda}}}^{+}{{\Omega }})_{m - 1/2}^{n + 1/2} \frac{{{\mathbf{u}}_m^{n + 1/2} - \frac{h}{2}{\mathbf{Q}}_{m - 1}^{n + 1/2} - {\mathbf{u}}_{m - 1}^{n + 1/2} - \frac{h}{2}{\mathbf{Q}}_{m - 1}^{n}}}{h} = 0. \\ \end{gather*}
Дальше >>
< Лекция 4 || Лекция 5: 123456789 || Лекция 6 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 30
Максим Радунцев
Максим Радунцев
Россия
предложить дружбу
Надежда Павленко
Надежда Павленко
Россия, Ставрополь
предложить дружбу