НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 5: Численное решение уравнений в частных производных гиперболического типа с большими градиентами решений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: профессионал | Доступ: платный

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать программу

5.3. Гибридные схемы и пространство неопределенных коэффициентов

Повышать точность метода также можно, если использовать разложение сеточной функции 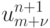$u_{m +{\nu}}^{n + 1}$ в ряд Тейлора в окрестности точки (tⁿ, x_m) . В общем случае любая разностная схема представляется в виде суммы по точкам шаблона с неопределенными весовыми множителями [15.8]:

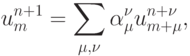${u_m^{n + 1} = \sum\limits_{{\mu},{\nu}} {{\alpha}_{\mu}^{\nu}}u_{{m} + {\mu}}^{{n} +{\nu}}, }$

( 5.2)

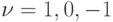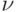где $\nu = 1, 0, - 1$ — номера слоев по времени, входящих в шаблон (шаблоны с более чем 3 слоями по времени рассматривать не будем), $\mu = 0, \pm 1, \pm 2, ..$ . - пространственные узлы точек сеточного шаблона $(t^{{n} +{\nu}}, x_{{m} + {\mu}} ),{\alpha}_{\mu}^\nu$ — неопределенные коэффициенты. Если $\nu$ не принимает положительных значений, то схема явная, в противном случае — неявная. Если все 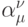${\alpha}_{\mu}^ \nu$ неотрицательные, то схема монотонная по Фридрихсу или схема с положительной аппроксимацией.

Учитывая продолжения исходного дифференциального уравнения

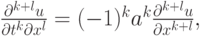
$\frac{{{\partial}^{{k} + l} u}}{{{\partial}t^{k} {\partial}x^l }} = (- 1)^{k} a^{k} \frac{{{\partial}^{{k} + l} u}}{{{\partial}x^{{k} + l}}},$

полученные дифференцированием исходного однородного уравнения переноса по независимым переменным k + l - 1 раз, получим после подстановки разложения проекции точного решения уравнения переноса на сетку 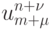$u_{m + {\mu}}^{n +{\nu}}$ в разностную схему (5.2):

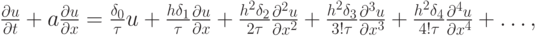${\frac{{\partial}u}{{\partial}t} + a \frac{{\partial}u}{{\partial}x} = \frac{{\delta_0 }}{\tau}u + \frac{{h \delta_1}}{\tau} \frac{{\partial}u}{{\partial}x} + \frac{{h^2 \delta_2}}{{2{\tau}}} \frac{{{\partial}^2 u}}{{{\partial}x^2}} + \frac{{h^2 \delta_3 }}{{3!{\tau}}} \frac{{{\partial}^3 u}}{{{\partial}x^3 }} + \frac{{h^2 \delta_4 }}{{4!{\tau}}} \frac{{{\partial}^4 u}}{{{\partial}x^4 }} + \ldots , }$

( 5.3)

откуда получим выражения для условий порядка, соблюдение которых необходимо для того, чтобы разностная схема аппроксимировала дифференциальную задачу

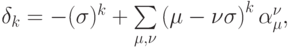
$\delta_k = - (\sigma)^{k} + \sum\limits_{{\mu},{\nu}}{\left({{\mu}- {\nu}{\sigma}}\right)^{k}{\alpha}_{\mu}^{\nu}},$

$\sigma = a\tau /h$ — число Куранта, k = 0, 1, 2, ... — порядок аппроксимации, который может быть достигнут.

Из условий аппроксимации видно, что для получения первого порядка точности 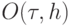$O(\tau , h)$ необходимо и достаточно выполнения условий

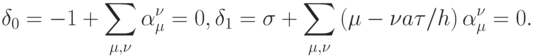${\delta_0 = - 1 + \sum\limits_{{\mu},{\nu}}{{\alpha}_{\mu}^{\nu}} = 0, \delta_1 = {\sigma}+ \sum\limits_{{\mu}, \nu}{\left({{\mu}-{\nu}a{\tau}/h}\right){\alpha}_{\mu}^{\nu}} = 0.}$

( 5.4)

Для получения схем более высокого порядка аппроксимации необходимо использовать условия порядка с более высокими k.

Для построения разностных схем с заданными свойствами в [15.9] предложено ввести линейное пространство неопределеннных коэффициентов $\left\{{{\alpha}_{\mu}^{\nu}}\right\}$ , в [15.10] на основе такого подхода предложена теория построения разностных схем повышенного порядка точности, в [15.6] - теория построения гибридных схем, наиболее близких в этом пространстве к монотонным по евклидовой норме.

Существует несколько определений монотонной схемы. Они, вообще говоря, не эквивалентны. Одно из определений приведено выше — это неотрицательность коэффициентов разностной схемы при записи в виде, разрешенном относительно точки (t^{n + 1}, x_m). Монотонная схема по Борису и Буку — схема, не увеличивающая число экстремумов в разностном решении задачи по сравнению с количеством экстремумов в точном решении задачи. Дадим еще одно определение монотонной схемы.

Определение.Схема называется монотонной, если из условия 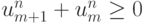$u_{m + 1}^{n} + u_m^{n} \ge 0$ следует 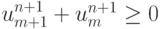$u_{m + 1}^{n + 1} + u_m^{n + 1} \ge 0$ для всех m.

Для системы уравнений в частных производных гиперболического типа

$\frac{{{\partial}{\mathbf{u}}}}{{\partial}t} + {\mathbf{A}} \frac{{{\partial}{\mathbf{u}}}}{{\partial}x} = 0,$

где $\mathbf{A}$ — квадратная матрица с постоянными коэффициентами размера $n \times n, {\mathbf{u}} = (u_1 , \ldots , u_n)^{T}$ — вектор - столбец, разностную схему можно представить в виде [15.11] (см. также "Введение в методы численного решения уравнений газовой динамики" ):

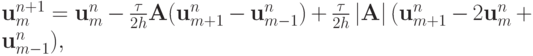
${\mathbf{u}}_m^{n + 1} = {\mathbf{u}}_m^{n} - \frac{\tau}{2h} {\mathbf{A}}({\mathbf{u}}_{m + 1}^{n} - {\mathbf{u}}_{m - 1}^{n} ) + \frac{\tau}{2h} \left| {\mathbf{A}}\right|({\mathbf{u}}_{m + 1}^{n} - 2{\mathbf{u}}_m^{n} + {\mathbf{u}}_{m - 1}^{n} ),$

или

$\begin{multline*} {\mathbf{u}}_m^{n + 1} = {\mathbf{u}}_m^{n} - \frac{\tau}{2h} \left\{\left({{{\Omega }}^{- 1}{{{\Lambda}\Omega }}}\right)({\mathbf{u}}_{m + 1}^{n} - {\mathbf{u}}_{m - 1}^{n})+\right. \\ \left. + \left({{{\Omega }}^{- 1} \left| {{{\Lambda}}}\right|{{\Omega }}}\right)({\mathbf{u}}_{m + 1}^{n} - 2{\mathbf{u}}_m^{n} + {\mathbf{u}}_{m - 1}^{n} )\right\}, \end{multline*}$

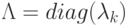где $\Lambda = diag(\lambda _{k})$ — диагональная матрица из собственных значений матрицы 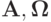$\mathbf{A, \Omega}$ — матрица размера n x n, строками которой являются левые собственные векторы матрицы $\mathbf{A}$ . Если матрица $\mathbf{A}$ невырожденная и все ее собственные числа действительны, то система имеет гиперболический тип, а матрица системы может быть представлена в виде произведения трех матриц ${\mathbf{A}} = {{\Omega }}^{- 1}{{\Lambda \Omega }}$ . Матрица перехода в базис из собственных векторов в данном случае есть матрица из левых собственных векторов матрицы системы, так как матрица $\mathbf{A}$ несамосопряженная. Обратную матрицу к матрице перехода также надо вычислять непосредственно — как правило, в задачах механики сплошных сред матрица перехода не ортогональная, обратная матрица не равна транспонированной.

Эту же схему можно записать в виде

${\mathbf{u}}_m^{n + 1} = {\mathbf{u}}_m^{n} - \frac{\tau}{h} \left\{{{\mathbf{A}}^{-} ({\mathbf{u}}_{m + 1}^{n} - {\mathbf{u}}_m^{n} ) + {\mathbf{A}}^{+}({\mathbf{u}}_m^{n} + {\mathbf{u}}_{m - 1}^{n} )}\right\},$

где ${\mathbf{A}}^{-} = 0, 5({\mathbf{A}} + \left| {\mathbf{A}}\right|), {\mathbf{A}}^{+} = 0, 5({\mathbf{A}} - \left| {\mathbf{A}}\right|)$ , или

${\mathbf{u}}_m^{n + 1} = {\mathbf{u}}_m^{n} - \frac{\tau}{h} \left\{{\left({{{\Omega }}^{- 1}{{\Lambda}}^{-}{\omega }}\right)({\mathbf{u}}_{m + 1}^{n} - {\mathbf{u}}_m^{n} ) - \left({{\omega }^{- 1}{{{\Lambda}}}^{+}{{\Omega }}}\right)({\mathbf{u}}_m^{n} + {\mathbf{u}}_{m - 1}^{n} )}\right\},$

где ${{\Lambda}}^{+} = 0, 5({{{\Lambda}}} - \left| {{\Lambda}}\right|), {{\Lambda}}^{-} = 0, 5({{{\Lambda}}} + \left| {{\Lambda}}\right|)$ ,

Если по аналогии со скалярными потоками 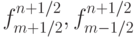$f_{m + 1/2}^{n + 1/2}, f_{m - 1/2}^{n + 1/2}$ ввести векторные потоки 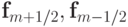${\mathbf{f}}_{m + 1/2}, {\mathbf{f}}_{m - 1/2}$ , то разностная схема (5.2) может быть представлена в виде:

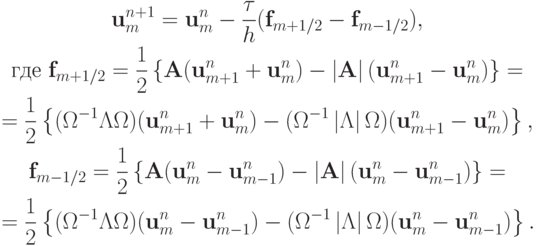
$\begin{gather*} {\mathbf{u}}_m^{n + 1} = {\mathbf{u}}_m^{n} - \frac{\tau}{h}({\mathbf{f}}_{m + 1/2} - {\mathbf{f}}_{m - 1/2} ), \\ \mbox{где }{\mathbf{f}}_{m + 1/2} = \frac{1}{2} \left\{{{\mathbf{A}}({\mathbf{u}}_{m + 1}^{n} + {\mathbf{u}}_m^{n} ) - \left| {\mathbf{A}}\right|({\mathbf{u}}_{m + 1}^{n} - {\mathbf{u}}_m^{n} )}\right\} = \\ = \frac{1}{2} \left\{{({{\Omega }}^{- 1}{{\Lambda \Omega }})({\mathbf{u}}_{m + 1}^{n} + {\mathbf{u}}_m^{n} ) - ({{\Omega }}^{- 1} \left| {{{\Lambda}}}\right|{{\Omega }})({\mathbf{u}}_{m + 1}^{n} - {\mathbf{u}}_m^{n} )}\right\}, \\ {\mathbf{f}}_{m - 1/2} = \frac{1}{2} \left\{{{\mathbf{A}}({\mathbf{u}}_m^{n} - {\mathbf{u}}_{m - 1}^{n} ) - \left|{\mathbf{A}}\right|({\mathbf{u}}_m^{n} - {\mathbf{u}}_{m - 1}^{n} )}\right\} = \\ = \frac{1}{2} \left\{{({{\Omega }}^{- 1}{{\Lambda \Omega }})({\mathbf{u}}_m^{n} - {\mathbf{u}}_{m - 1}^{n} ) - ({{\Omega }}^{ - 1} \left| {{{\Lambda}}}\right|{{\Omega }})({\mathbf{u}}_m^{n} - {\mathbf{u}}_{m - 1}^{n} )}\right\}. \end{gather*}$

Для одномерной квазилинейной системы уравнений газовой динамики разностная схема выписана подробно в "Введение в методы численного решения уравнений газовой динамики" . В квазилинейном случае потоки 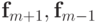${\mathbf{f}}_{m + 1}, {\mathbf{f}}_{m - 1}$ можно представить в виде

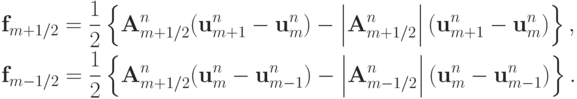
$\begin{gather*} {\mathbf{f}}_{m + 1/2} = \frac{1}{2} \left\{{{\mathbf{A}}_{m + 1/2}^{n}({\mathbf{u}}_{m + 1}^{n} - {\mathbf{u}}_m^{n} ) - \left| {{\mathbf{A}}_{m + 1/2}^{n}}\right|({\mathbf{u}}_{m + 1}^{n} - {\mathbf{u}}_m^{n} )}\right\}, \\ {\mathbf{f}}_{m - 1/2} = \frac{1}{2} \left\{{{\mathbf{A}}_{m + 1/2}^{n} ({\mathbf{u}}_m^{n} - {\mathbf{u}}_{m - 1}^{n} ) - \left|{{\mathbf{A}}_{m - 1/2}^{n}}\right|({\mathbf{u}}_m^{n} - {\mathbf{u}}_{m - 1}^{n} )}\right\}. \end{gather*}$

Матрицы, входящие в приведенные выше формулы, выписаны в "Введение в методы численного решения уравнений газовой динамики" .

Дальше >>

Численные методы решения уравнений в частных производных

Численные методы решения уравнений в частных производных

Лекция 5: Численное решение уравнений в частных производных гиперболического типа с большими градиентами решений

5.3. Гибридные схемы и пространство неопределенных коэффициентов

Вопросы и ответы

Студенты

Авторизоваться

Численные методы решения уравнений в частных производных

Численные методы решения уравнений в частных производных

Лекция 5: Численное решение уравнений в частных производных гиперболического типа с большими градиентами решений

5.3. Гибридные схемы и пространство неопределенных коэффициентов

Вопросы и ответы

Студенты