Численные методы решения уравнений в частных производных

:

Численные методы решения уравнений в частных производных
[+]

Лекция 5: Численное решение уравнений в частных производных гиперболического типа с большими градиентами решений

A
|
версия для печати
< Лекция 4 || Лекция 5: 123456789 || Лекция 6 >

5.10. TVD - схемы для линейных систем уравнений гиперболического типа

Построим разностную схему типа TVD для случая одномерной системы линейных уравнений в частных производных гиперболического типа, к которым относятся, например, системы уравнений акустики или теории упругости.

Запишем систему как и ранее в матричной форме представления

$ \frac{{{\partial}{\mathbf{u}}}}{{\partial}t} + {\mathbf{A}} \frac{{{\partial}{\mathbf{u}}}}{{\partial}x} = 0, $

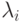где u — вектор - столбец искомых функций, \mathbf{A} — квадратная матрица n x n с постоянными коэффициентами, t, x — независимые переменные. Пусть матрица \mathbf{A} имеет n действительных собственных чисел \lambda _{i} и собственных векторов 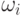\omega _{i}. Без ограничения общности можно считать, что среди этих собственных чисел нет кратных, а соответствующие собственные вектора образуют базис.

Тогда возможен переход к базису из собственных векторов, в котором матрица системы диагонализуется, сама система запишется как

$ \frac{{{\partial}{\mathbf{u}}}}{{\partial}t} + {{\Omega }}^{- 1}{{\Lambda \Omega }} \frac{{{\partial}{\mathbf{u}}}}{{\partial}x} = 0, $

где \Lambda — диагональная матрица из собственных чисел матрицы \mathbf{A}, \Omega — матрица, строками которой являются соответствующие левые собственные векторы. Последнее уравнение можно переписать следующим образом:

$ \frac{{{\partial}{\mathbf{R}}}}{{\partial}t} + {{{\Lambda}}} \frac{{\partial {\mathbf{R}}}}{{\partial}x} = 0, $

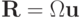где {\mathbf{R}} = {\Omega \mathbf{u}} — инварианты Римана.

Разностную схему для численного решения уравнения в инвариантах представим в виде:

\begin{gather*} {\mathbf{R}}_m^{n + 1} = {\mathbf{R}}_m^{n} - {\sigma}({\mathbf{\tilde{f}}}_{m + 1/2} - {\mathbf{\tilde{f}}}_{m - 1/2}), \\ {\mathbf{\tilde{f}}}_{m \pm 1/2} = \frac{1}{2}({\mathbf{f}}_m + {\mathbf{f}}_{m + 1} + {{\Omega }}_{m + 1/2} \varphi_{m + 1/2} ). \end{gather*}

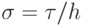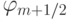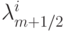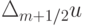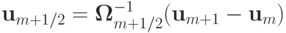Здесь \sigma = \tau /h, а \varphi_{m + 1/2} вычисляется аналогично скалярному случаю, с учетом того, что вместо am + 1/2 необходимо брать \lambda_{m + 1/2}^{i}, i — номер собственного значения, вместо \Delta _{m + 1/2}u: {\mathbf{u}}_{m + 1/2} = {\mathbf{\Omega}}_{m + 1/2}^{- 1} ({\mathbf{u}}_{m + 1} - {\mathbf{u}}_m ).

Явную схему TVD второго порядка точности типа предиктор - корректор для численного решения нелинейной системы уравнений гиперболического типа представим в виде:

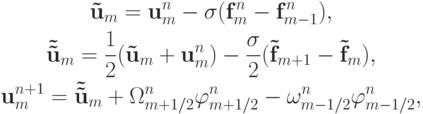
\begin{gather*} {\mathbf{\tilde{u}}}_m = {\mathbf{u}}_m^{n} - {\sigma}({\mathbf{f}}_m^{n} - {\mathbf{f}}_{m - 1}^{n} ), \\ {\mathbf{\tilde{\tilde{u}}}}_m = \frac{1}{2}({\mathbf{\tilde{u}}}_m + {\mathbf{u}}_m^{n}) - \frac{\sigma }{2}({\mathbf{\tilde{f}}}_{m + 1} - {\mathbf{\tilde{f}}}_m ), \\ {\mathbf{u}}_m^{n + 1} = {\mathbf{\tilde{\tilde{u}}}}_m + {{\Omega }}_{m + 1/2}^{n} \varphi_{m + 1/2}^{n} - {\omega }_{m - 1/2}^{n} \varphi_{m - 1/2}^{n} , \end{gather*}

где компоненты вектора

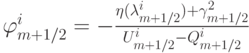
$ \varphi_{m + 1/2}^{i} = - \frac{{\eta (\lambda_{m + 1/2}^{i} ) + \gamma_{m + 1/2}^2}}{{U_{m + 1/2}^{i} - Q_{m + 1/2}^{i}}} $
.

Функция, входящая в выражение для лимитера, вычисляется

Q_{m + 1/2} = \left\{ \begin{array}{l} \min\bmod ({\mathbf{u}}_{m + 1/2}, {\mathbf{u}}_{m - 1/2} ) + \\ + \min\bmod ({\mathbf{u}}_{m + 1/2}, {\mathbf{u}}_{m + 3/2}) - {\mathbf{u}}_{m + 1/2},\\ {\min\bmod ({\mathbf{u}}_{m + 1/2}, {\mathbf{u}}_{m - 1/2}, {\mathbf{u}}_{m + 3/2} ), } \\ {\min\bmod (2{\mathbf{u}}_{m - 1/2}, 2{\mathbf{u}}_{m + 1/2}, 2{\mathbf{u}}_{m + 3/2}, 0, 5({\mathbf{u}}_{m - 1/2} + {\mathbf{u}}_{m + 3/2} ))} . \\ \end{array} \right.
Дальше >>
< Лекция 4 || Лекция 5: 123456789 || Лекция 6 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 30
Максим Радунцев
Максим Радунцев
Россия
предложить дружбу
Надежда Павленко
Надежда Павленко
Россия, Ставрополь
предложить дружбу