НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 5: Численное решение уравнений в частных производных гиперболического типа с большими градиентами решений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: профессионал | Доступ: платный

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать программу

5.7. Разностные схемы для квазилинейного уравнения переноса

Рассмотрим теперь нелинейное уравнение переноса, записанное в дивергентной форме

${\frac{{\partial}u}{{\partial}t} + \frac{{{\partial}f(u)}} {{\partial}x} = 0}$

( 5.5)

и соответствующей характеристической форме, которая легко получается из дивергентной:

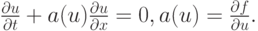${\frac{{\partial}u}{{\partial}t} + a(u) \frac{{\partial}u} {{\partial}x} = 0, a(u) = \frac{{\partial}f}{{\partial}u}.}$

( 5.6)

В дивергентной форме записи этого квазилинейного уравнения переноса величина f играет роль потока. Представим явную трехточечную разностную схему для численного решения (5.5) или (5.6) в потоковой форме

${u_m^{n + 1} = u_m^{n} - \bar{\sigma} (f_{{m} + 1/2}^{n} - f_{{m} - 1/2}^{n} ), }$

( 5.7)

где

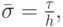
$\bar{\sigma}= \frac{\tau}{h},$

$\begin{gather*} f_{{m} + 1/2}^{n} = \frac{1}{2} \left[{f_m^{n} + f_{{m} + 1}^{n} - \eta (a_{{m} + 1/2} ) \cdot \Delta u_{{m} + 1/2}}\right], \\ f_{{m} - 1/2}^{n} = \frac{1}{2} \left[{f_{m - 1}^{n} + f_m^{n} - \eta (a_{{m} - 1/2} ) \cdot \Delta u_{{m} - 1/2}}\right], \\ {\Delta}u_{{m} + 1/2} = u_{{m} + 1} - u_m , \quad {\Delta}u_{{m} - 1/2} = u_m - u_{{m} - 1/2}, \end{gather*}$

$\eta$ — коэффициент при второй разности в разностной схеме, если a = const.

В случае схемы Куранта - Изаксона - Риса (или схемы с разностями, ориентированными против потока — upwind scheme) имеем

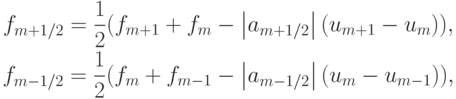
$\begin{gather*} f_{{m} + 1/2} = \frac{1}{2}(f_{{m} + 1} + f_m - \left| {a_{{m} + 1/2}}\right|(u_{{m} + 1} - u_m )), \\ f_{{m} - 1/2} = \frac{1}{2}(f_m + f_{m - 1} - \left| {a_{{m} - 1/2}}\right|(u_m - u_{m - 1} )), \end{gather*}$

для сокращения записи введена скорость переноса, вычисляемая по формуле

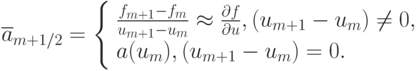
$\overline{a}_{m + 1/2} = \left\{ \begin{array}{l} {\frac{f_{m + 1} - f_m}{u_{m + 1} - u_m} \approx \frac{{\partial}f}{{\partial}u}, (u_{m + 1} - u_m) \ne 0 }, \\ {a(u_m), (u_{m + 1} - u_m) = 0 } . \\ \end{array} \right.$

В квазилинейном случае совпадавшие в линейном случае схемы будут приводить к разным разностным уравнениям, соответственно, будут различаться и численные решения из - за разности погрешностей аппроксимации. В случае квазилинейного уравнения для схемы Лакса - Вендроффа выражения для потоков будут иметь следующий вид:

$\begin{gather*} f_{{m} + 1/2} = \frac{1}{2} \left[{f_{{m} + 1} + f_m - \frac{\tau}{h}a_{{m} + 1/2}^2 (u_{{m} + 1} - u_m )}\right], \\ f_{{m} - 1/2} = \frac{1}{2} \left[{f_m + f_{m - 1} - \frac{\tau}{h}a_{{m} - 1/2}^2 (u_m - u_{m - 1} )}\right]. \end{gather*}$

Для схем Куранта - Изаксона - Риса и Лакса - Вендроффа коэффициенты $\eta (a_{m \pm 1/2})$ будут иметь значения $| a_{m \pm 1/2} |$ и

$\frac{\tau}{h} (a_{{m} \pm 1/2} )^2$

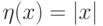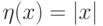соответственно. Если, например, функция $\eta (x) = | x |$ при $| x | \approx \varepsilon$ , где $\varepsilon$ — малое число (порядка величины аппроксимационной вязкости для разностной схемы первого порядка Куранта - Изаксона - Риса), то полагают $\eta (x) = | x |$ при

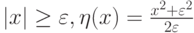
$\left|{x}\right| \ge \varepsilon , \eta (x) = \frac{{x^2 + {\varepsilon}^2 }}{{2\varepsilon }}$

при $| x | < \varepsilon$ .

Введем обозначение $\gamma_{m + 1/2} = 2\bar{\sigma} a_{m + 1/2}$ , тогда величины потоков $f_{m \pm 1/2}$ можно переписать как

$\begin{gather*} \bar{\sigma} f_{{m} + 1/2} = \bar{\sigma} f_m - \frac{1}{2} \left[{- \gamma_{{m} + 1/2} + Q(\gamma_{{m} + 1/2})}\right] \Delta_{{m} + 1/2} u, \\ \bar{\sigma} f_{{m} - 1/2} = \bar{\sigma} f_m - \frac{1}{2} \left[{\gamma_{{m} - 1/2} + Q(\gamma_{{m} - 1/2} )}\right] \Delta_{{m} - 1/2} u. \end{gather*}$

Здесь введены обозначения

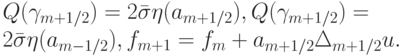
$Q(\gamma_{m + 1/2} ) = 2 \bar{\sigma} \eta (a_{m + 1/2} ), Q(\gamma_{m + 1/2} ) =\\ 2 \bar{\sigma} \eta (a_{{m} - 1/2} ), f_{m + 1} = f_m + a_{m + 1/2} \Delta_{m + 1/2} u.$

Подставляя эти выражения для численных потоков в (5.7), получаем

${u_m^{n + 1} = u_m^{n} + C_{{m} + 1/2}^{+}\Delta_{{m} + 1/2} \cdot u^{n} - C_{{m} - 1/2}^{-}\Delta_{{m} - 1/2} u^{n}, }$

( 5.8)

где

$C_{{m} + 1/2}^{+} = \frac{1}{2} \left[{Q(\gamma_{{m} + 1/2} ) - \gamma_{{m} + 1/2}}\right], C_{{m} + 1/2}^{-} = \frac{1}{2} \left[{Q(\gamma_{{m} + 1/2} ) + \gamma_{{m} + 1/2}}\right],$

откуда следует

$C_{{m} + 1/2}^{+} + C_{{m} + 1/2}^{-} = Q (\gamma_{{m} + 1/2} ).$

В случае линейного уравнения переноса с постоянным коэффициентом (постоянной скоростью переноса) 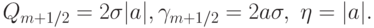$Q_{m + 1/2} = 2\sigma | a |, \gamma _{m + 1/2} = 2a\sigma ,\ \eta = | a |.$ Условие устойчивости такой схемы имеет вид

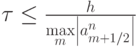
${\tau} \le \frac{h}{{\max\limits_m \left| {a_{{m} + 1/2}^{n}}\right|}}$

Построенная разностная схема относится к классу TVD - схем, что непосредственно проверяется. Схема обеспечивает выполнение условия 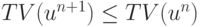${TV}(u^{n + 1} ) \le TV(u^n)$ с учетом неравенств 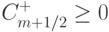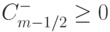$C_{{m} + 1/2}^ + \ge 0$ , ${C_{{m} - 1/2}^{-} \ge 0}$ , $C_{{m} + 1/2}^{+} + C_{{m} + 1/2}^{-} \le 1$ для любых m.