НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: профессионал | Доступ: платный

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать программу

1.3. Элементы теории устойчивости разностных схем

Канонической формой двухслойной линейной разностной схемы называется ее запись в виде

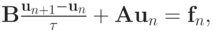${\mathbf{B} \frac{\mathbf{u}_{n + 1} - \mathbf{u}_n}{\tau} + \mathbf{Au}_n = \mathbf{f}_n , }$

( 1.1)

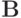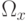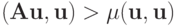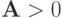$\mathbf{B}$ и $\mathbf{A}$ — операторы, действующие в $\Omega _{x}$ . Рассматриваем случай , когда для этих операторов выполнено условие $(\mathbf{Au}, \mathbf{u}) > \mu(\mathbf{u}, \mathbf{u})$ , где $\mu$ — положительное число, $\mathbf{u}$ — произвольный ненулевой элемент пространства сеточных функций. Тогда оператор $\mathbf{A}$ называется положительным, записывается $\mathbf{A} > 0$ . Требуем и 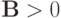$\mathbf{B} > 0$ . Пока не оговорено иное, рассматриваем случаи самосопряженных операторов.

Если $\mathbf{B} = \mathbf{E}$ , то разностная схема называется явной. Рассмотрим для примера разностную схему с весами для одномерного уравнения теплопроводности

$\frac{{u_m^{n + 1} - u_m^{n}}}{\tau} = \xi \mathbf{\Lambda}}_{xx} u_m^{n + 1} + (1 - \xi ){\mathbf{\Lambda}}_{xx}u_m^{n}, \xi \in \left[{0, 1}\right],$

где

$\begin{gather*} {\mathbf{\Lambda}}_{xx} u_m^{n + 1} = \frac{u_{m - 1}^{n + 1} - 2u_m^{n + 1} + u_{m + 1}^{n + 1}}{h^2}, {\mathbf{\Lambda}}_{xx} u_m^{n} = \frac{u_{m - 1}^n - 2u_m^n + u_{m + 1}^n}{h^2}, \\ n = 0, \ldots , N - 1 , \quad m = 0, \ldots , M - 1. \end{gather*} $$

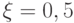В случае $\xi = 0, 5$ эта схема называется схемой Кранка - Никольсон. Для записи схемы с весами в каноническом виде положим

${\mathbf{Au}}_n = - {\mathbf{\Lambda}}_{xx} u_m^{n}, {\mathbf{Au}}_{n + 1} = - {\mathbf{\Lambda}}_{xx} u_m^{n + 1},$

и, обозначив 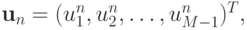$\mathbf{u}_n = (u_1^{n}, u_2^{n}, \ldots , u_{M - 1}^{n})^T ,$ получим форму записи

$\mathbf{B} \frac{\mathbf{u}_{n + 1} - \mathbf{u}_n}{\tau} + \mathbf{Au}_n = 0,$

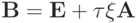где ${\mathbf{B}} = {\mathbf{E}} +{\tau}\xi {\mathbf{A}}$ .

В случае неравномерной сетки каноническая форма записи схемы будет

${\mathbf{B} \frac{{{\mathbf{u}}_{n + 1} - {\mathbf{u}}_n }}{{\tau_{n + 1}}} + \mathbf{A} {\mathbf{u}}_n = {\mathbf{f}}_n , \quad {\mathbf{f}}_n = (f_1^{n}, \ldots , f_{M - 1}^{n} )^T.}$

( 1.2)

Иногда схему с весами записывают в виде

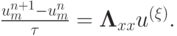
$\frac{{u_m^{n + 1} - u_m^{n}}}{\tau} = {\mathbf{\Lambda}}_{xx}u^{(\xi )}.$

Заметим, что канонический вид разностной схемы аналогичен итерационному методу решения СЛАУ 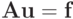$\mathbf{Au} = \mathbf{f}$ . Эта аналогия не является формальной — переход от СЛАУ к итерационному методу (1.1) может быть интерпретирован , как замена стационарного уравнения 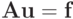$\mathbf{Au} = \mathbf{f}$ нестационарным. Решение последнего при стационарных граничных условиях стремится к решению стационарного при стремлении времени к бесконечности.

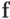Отличие состоит в том, что в последнем случае операторы $\mathbf{B}, \mathbf{A}$ и функция $\mathbf{f}$ не зависят от n и итерационный параметр $\tau$ не обязательно должен стремиться к нулю.

Введем величину $({\mathbf{Au}}, {\mathbf{u}})$ — энергию оператора $\mathbf{A}$ , а также энергетическую норму вектора:

$\|{\mathbf{u}}\|_{\mathbf{A}} = ({\mathbf{Au}}, {\mathbf{u}})^{1/2}.$

Говорят, что эта норма порождается оператором $\mathbf{A}$ .

Рассматривается задача Коши для оператора — однородного разностного уравнения (1.1); ${\mathbf{u}}^0 = {\varphi}$ .

Дадим два определения.

Определение 6. Разностная схема (1.1) устойчива по начальным данным, если для решения (1.1) выполняется оценка:

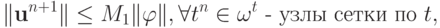${\|{\mathbf{u}}^{n + 1}\| \le M_1 \| {\varphi}\| , {\forall}t^{n} \in {\omega}^{t} \mbox{ - узлы сетки по } t, }$

( 1.3)

причем константа M₁ не зависит от сеточных параметров.

Будем рассматривать также неоднородное уравнение, соответствующее (1.1):

${{\mathbf{B}} \frac{{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n}}}{\tau} = - {\mathbf{Au}}^{n} + {\mathbf{f}}(x_m , t^{n}).}$

( 1.4)

Определение7. Говорят, что разностная схема (1.4) устойчива по правой части, если для решения (1.4) в любой момент времени выполняется условие

${\|{\mathbf{u}}^{n + 1}\| \le M_2 \|{\mathbf{f}}\| , }$

( 1.5)

причем константа M₂ не зависит от сеточных параметров.

Определение 8. Разностная схема (1.1) равномерно устойчива по начальным данным в энергетической норме, порождаемой некоторым оператором 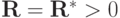${\mathbf{R}} = {\mathbf{R}}^* > 0$ , если 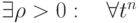${\exists}{\rho} > 0: \quad {\forall}t^{n}$ выполнено:

$\|\mathbf{u}_{n + 1}\|_{\mathbf{R}} \le {\rho}\|\mathbf{u}_n \|_{\mathbf{R}}$

и при этом 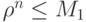${\rho}^{n} \le M_1$ , $\rho$ и M₁ не зависят от сеточных параметров.

Обычно рассматриваются случаи 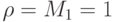$\rho = M_{1} = 1$ или $\rho = 1 + c\tau$ , M₁ = e^cT.

Если разностную схему в каноничной форме представить в виде

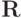${\mathbf{u}}_{n + 1} = {\mathbf{R}}_{\tau}{\mathbf{u}}_n +{\tau}{\mathbf{B}}^{- 1}{\mathbf{f}}_n , n = 0, \ldots , N - 1 , {\mathbf{R}}_{\tau} = {\mathbf{R}}_{\tau}(t_n ),$

то оператор ${\mathbf{R}}_{\tau} = {\mathbf{E}} -{\tau}{\mathbf{B}}^{- 1} {\mathbf{A}}$ называется оператором послойного перехода разностной схемы (1.1). 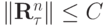Нетрудно заметить, что условие равномерной устойчивости по начальным данным эквивалентно ограничению нормы оператора ${\mathbf{R}}_{\tau}$ : $\left\| {{\mathbf{R}}_{\tau}}\right\| \le {\rho}$ , а в силу условия $\rho^{n} \le C$ и ограниченности норм степеней оператора $\mathbf{R}$ : $\left\| {{\mathbf{R}}_{\tau}^{n}}\right\| \le C$ .

Для оценки нормы оператора 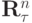${\mathbf{R}}_{\tau}^{n}$ можно воспользоваться собственными значениями этого оператора — корнями уравнения $\det \| {{\mathbf{R}}_{\tau} - {\lambda}{\mathbf{E}}}\| = 0$ .

Если $\lambda$ — собственное значение, а $\omega$ — соответствующий ему собственный вектор, то ${\mathbf{R}}_{\tau}{{\omega }} = {\lambda}{{\omega }}$ . Поэтому ${\mathbf{R}}^{n}_{\tau}{\omega} = \lambda^{n}{{\omega }}$ , откуда $\left\| {{\mathbf{R}}_{\tau}^{n}}\right\| \ge \left| {\lambda}\right|^{n}$ , так как $\left\| {{\mathbf{R}}_{\tau}^{n}{{\omega }}}\right\| = \left| {\lambda}\right|^{n} \left\| {{\omega }}\right\| \le \left\|{{\mathbf{R}}_{\tau}^{n}}\right\| \left\|{{\omega }}\right\|$ .

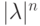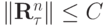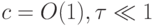Последнее неравенство должно выполняться при любом n. Оно невыполнимо, если $| \lambda |^{n}$ с увеличением n будет неограниченно расти, так как $\left\| {{\mathbf{R}}_{\tau}^{n}}\right\| \le C$ . Этого не произойдет, если на $\lambda$ будет наложено условие $\left| {\lambda}\right| \le 1 + c{\tau}$ , константа C не зависит от сеточных параметров , $c = O(1),{\tau}\ll 1$ . Последнее условие называется необходимым спектральным признаком устойчивости (признак фон Неймана).

Рассмотрим разностную задачу Коши для линейного уравнения переноса

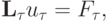
${\mathbf{L}}_{\tau} u_{\tau} = F_{\tau},$

где

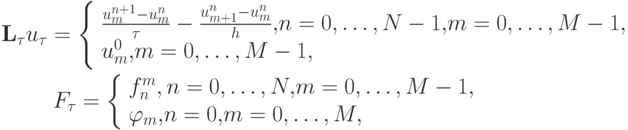
$\begin{gather*} \mathbf{L}_{\tau}u_{\tau} = \left\{ \begin{array}{l} {\frac{u_m^{n + 1} - u_{m }^{n}}{\tau} - \frac{u_{m + 1}^{n} - u_m^{n}}{h}, }{n = 0, \ldots , N - 1 , }{m = 0, \ldots , M - 1 , } \\ {u^0_m , }{m = 0, \ldots , M - 1 , } \\ \end{array} \right. \\ F_{\tau} = \left\{ \begin{array}{l} {f_n^{m}}, {n = 0, \ldots , N , }{m = 0, \ldots , M - 1 , } \\ {\varphi_m , }{n = 0, }{m = 0, \ldots , M , } \\ \end{array} \right. \end{gather*}$

Условие ее устойчивости записывается в виде неравенства

$\|u_{\tau}\| \le C \|F_{\tau}\|.$

Для однородного уравнения переноса это условие принимает вид

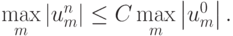
$\max\limits_m \left| {u_m^{n}}\right| \le C \max\limits_m \left| {u_m^0 } \right|.$

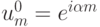Последнее неравенство означает устойчивость разностной схемы по начальным данным. Оно должно выполняться, в частности, в случае, если $u_m^0 = \varphi_n$ является произвольной гармоникой при представлении начальных условий в виде ряда Фурье (важно лишь знать, будет ли эта гармоника неограниченно расти по времени). Возьмем в качестве начального условия произвольную гармонику $u_m^0 = e^{i {\alpha}m}$ , где $\alpha$ — вещественный параметр.

Решение однородной разностной задачи в этом случае ищется с помощью метода разделения переменных. На каждом временном слое решение разностной задачи ищется как произведение 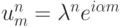$u_m^{n} = {\lambda}^{n} e^{i {\alpha}m}$ .

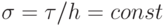Спектр оператора послойного перехода $\lambda(\alpha)$ легко ищется подстановкой в разностное уравнение. Например, для однородного уравнения переноса с постоянными коэффициентами после преобразований $u_m^{n + 1} = (1 - {\sigma})u_m^{n} + {\sigma}u_{m + 1}^{n}$ , где $\sigma = \tau /h = const$ — безразмерный параметр — число Куранта (в числитель дроби входит скорость переноса, которая в рассматриваемой задаче равна единице). Для спектра оператора перехода имеем ${\lambda}({\alpha}) = (1 - {\sigma}) + {\sigma}e^{i {\alpha}}$ .

Для решения вида 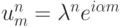$u_m^{n} = {\lambda}^{n} e^{i {\alpha}m}$ справедливо 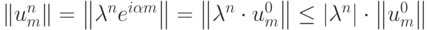$\left\| {u_m^{n}}\right\| = \left\| {{\lambda}^{n}e^{i {\alpha}m}}\right\| = \left\| {{\lambda}^{n} \cdot u_m^0 }\right\| \le \left| {{\lambda}^{n}}\right| \cdot \left\| {u_m^0 }\right\|$ , или $\max\limits_m \left| {u_m^{n}}\right| = \left| {{\lambda}^{n}}\right| \cdot \max\limits_m \left| {u_m^0 }\right|$ , поэтому для выполнения условия устойчивости $\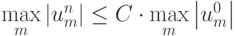max\limits_m \left| {u_m^{n}}\right| \le C \cdot \max\limits_m \left| {u_m^0 }\right|$ необходимо выполнение неравенства $| \lambda(\alpha)|^{n} \le 1 + C \tau$ .

Константа в правой части последнего неравенства не зависит от сеточных параметров.

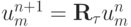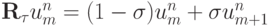Спектральным признаком это условие называется потому, что каждая гармоника $e^{i {\alpha}m}$ является собственной функцией оператора послойного перехода $u_m^{n + 1} = {\mathbf{R}}_{\tau} u_m^{n}$ . В частности, для рассмотренного выше примера с уравнением переноса ${\mathbf{R}}_{\tau} u_m^{n} = (1 - {\sigma})u_m^{n} + {\sigma}u_{m + 1}^{n}$ .

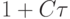Множество точек ${\lambda}(\alpha)$ на комплексной плоскости состоит из собственных значений оператора перехода — спектр оператора. При этом считаем ${\alpha}\in [0, 2 \pi ]$ . Сформулируем теперь спектральный признак устойчивости в этих терминах. Спектр оператора перехода с n на n + 1 временной слой должен лежать в круге радиуса $1 + C\tau$ на комплексной плоскости.

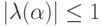В приведенном примере спектр оператора не зависит явно от $\tau$ поэтому условие устойчивости может быть записано в виде $\left| {{\lambda}({\alpha})}\right| \le 1$ .

Такое условие иногда называется условием строгой устойчивости. В [11.6] показано, что строго устойчивые схемы можно построить лишь для таких дифференциальных задач , для которых справедлив принцип максимума, т.е. максимальное и минимальное значения решение дифференциальной задачи принимает на границе расчетной области.

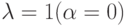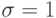Вернемся к модельному уравнению переноса. В данном случае спектр представляет собой окружность с центром в точке $(1 - \sigma )$ и радиусом $\sigma$ на комплексной плоскости. При $\sigma < 1$ эта окружность лежит внутри единичного круга, касаясь его в точке ${\lambda} = 1 ({\alpha} = 0)$ , при $\sigma = 1$ совпадает с единичной окружностью, при $\sigma > 1$ находится вне единичного круга.

Приведем еще один пример исследования на устойчивость разностной задачи:

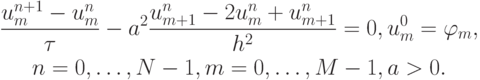
$\begin{gather*} \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} - a^2 \frac{{u_{m + 1}^{n} - 2u_m^{n} + u_{m + 1}^{n}}}{{h^2}} = 0, u_m^0 = \varphi_m , \\ n = 0, \ldots , N - 1 , m = 0, \ldots , M - 1 , a > 0. \end{gather*}$

Эта схема аппроксимирует задачу Коши для уравнения теплопроводности.

После подстановки решения в виде гармоники Фурье, умноженной на коэффициент перехода, 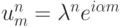$u_m^{n} = {\lambda}^{n} e^{i {\alpha}m}$ в разностное уравнение, получим уравнение для спектра оператора послойного перехода

$\frac{{\lambda}- 1}{\tau} - a \frac{e^{- i {\alpha}} - 2 + e^{i {\alpha}}}{h^2} = 0.$

Дальше >>

Численные методы решения уравнений в частных производных

Численные методы решения уравнений в частных производных

Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость

1.3. Элементы теории устойчивости разностных схем

Вопросы и ответы

Студенты

Авторизоваться

Численные методы решения уравнений в частных производных

Численные методы решения уравнений в частных производных

Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость

1.3. Элементы теории устойчивости разностных схем

Вопросы и ответы

Студенты