Численные методы решения уравнений в частных производных

:

Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Уровень: профессионал | Доступ: платный

Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость

A
|
версия для печати
Лекция 1: 1234567891011 || Лекция 2 >

После очевидных преобразований получим

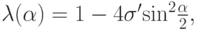
$ {\lambda}({\alpha}) = 1 - 4 \sigma^{\prime}{\sin}^2 \frac{{\alpha}}{2}, $

где 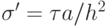\sigma ' = \tau a/h^{2} — аналог числа Куранта для параболических уравнений (иногда его называют параболическим числом Куранта)

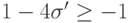При изменении \alpha спектр \lambda(\alpha) пробегает значения {1 - 4 \sigma^{\prime} \le {\lambda}({\alpha}) \le 1}, а для выполнения условия устойчивости необходимо 1 - 4 \sigma^{\prime} \ge - 1, или \sigma^{\prime} \le 1/2, откуда

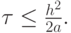
${\tau}\le \frac{h^2}{2a}. $

Аппроксимация этого же дифференциального уравнения с помощью неявной схемы приводит к следующему выражению для спектра \lambda(\alpha):

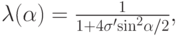
$ {\lambda}({\alpha}) = \frac{1}{1 + 4 \sigma^{\prime}{\sin}^2{\alpha}/2}, $

здесь, как и ранее, 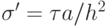\sigma ' = \tau a/h^{2}.

В этом случае условие устойчивости выполнено при любом соотношении сеточных параметров. В таких случаях говорят, что схема безусловно устойчивая.

Теорема 3. Для задачи Коши

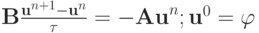$ {{\mathbf{B}} \frac{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^n}{\tau} = - {\mathbf{Au}}^n ; {\mathbf{u}}^0 = \varphi} $ ( 1.6)

условие

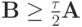
$ {\mathbf{B}} \ge \frac{\tau}{2}{\mathbf{A}} $
необходимо и достаточно для устойчивости в энергетической норме, порождаемой {\mathbf{A}}, т. е.

\|{\mathbf{u}}^{n + 1}\|_{\mathbf{A}} \le \|{\mathbf{u}}^0 \|_{\mathbf{A}}.

Неравенство в последней теореме имеет смысл операторного неравенства, т.е. для любого ненулевого вектора выполнено

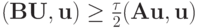
$ (\mathbf{BU}, \mathbf{u}) \ge \frac{\tau}{2}(\mathbf{Au}, \mathbf{u}) $
.

Доказательство. Достаточность. Умножим (1.6) скалярно на

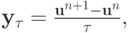
$ {\mathbf{y}}_{\tau} = \frac{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^n}{\tau}, $
тогда получим

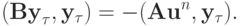
({\mathbf{By}}_{\tau}, {\mathbf{y}}_{\tau} ) = - ({\mathbf{Au}}^n , {\mathbf{y}}_{\tau} ).

Ввиду того, что

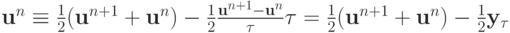
$ \mathbf{u}^{n} \equiv \frac{1}{2} (\mathbf{u}^{n + 1} + \mathbf{u}^{n}) - \frac{1}{2} \frac{\mathbf{u}^{n + 1} - \mathbf{u}^{n}}{\tau}{\tau} = \frac{1}{2}(\mathbf{u}^{n + 1} + \mathbf{u}^{n}) - \frac{1}{2} \mathbf{y}_{\tau} $

последнее равенство можно представить как уравнение:

$ {\left({\left({{\mathbf{B}} - \frac{\tau}{2}{\mathbf{A}}}\right){\mathbf{y}}_{\tau}, {\mathbf{y}}_{\tau}}\right) + \frac{1}{{2{\tau}}}({\mathbf{A}}({\mathbf{u}}^{n + 1} + {\mathbf{u}}^{n} ), {\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n} ) = 0.} $ ( 1.7)

В силу самосопряженности {\mathbf{A}}, ({\mathbf{Au}}^{n}, {\mathbf{u}}^{n + 1} ) = ({\mathbf{Au}}^{n + 1}, {\mathbf{u}}^{n} ) и тогда

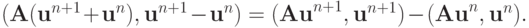
({\mathbf{A}}({\mathbf{u}}^{n + 1} + {\mathbf{u}}^{n} ), {\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n} ) = ({\mathbf{Au}}^{n + 1}, {\mathbf{u}}^{n + 1} ) - ({\mathbf{Au}}^{n}, {\mathbf{u}}^{n} ).

Из (1.7) следует

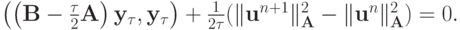$ {\left({\left({{\mathbf{B}} - \frac{\tau}{2}{\mathbf{A}}}\right){\mathbf{y}}_{\tau}, {\mathbf{y}}_{\tau}}\right) + \frac{1}{{2{\tau}}}(\|{\mathbf{u}}^{n + 1}\|_{\mathbf{A}}^2 - \|{\mathbf{u}}^{n}\|_{\mathbf{A}}^2 ) = 0.} $ ( 1.8)

В случае

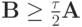
$ {\mathbf{B}} \ge \frac{\tau}{2}{\mathbf{A}}
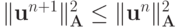получим, что \|{\mathbf{u}}^{n + 1}\|_{\mathbf{A}}^2 \le \|{\mathbf{u}}^{n}\|_{\mathbf{A}}^2 $. Отсюда следует устойчивость в норме 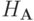H_{\mathbf{A}} по начальным данным.

Необходимость. Пусть \|{\mathbf{u}}^{n + 1}\|_{\mathbf{A}} \le \|{\mathbf{u}}^0 \|_{\mathbf{A}}. Используем равенство (1.7) (оно называется энергетическим тождеством ). В случае n = 0 из (1.7) следует:

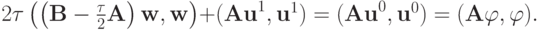
$ 2{\tau}\left({\left({{\mathbf{B}} - \frac{\tau}{2}{\mathbf{A}}}\right){\mathbf{w}}, {\mathbf{w}}}\right) + ({\mathbf{Au}}^1 , {\mathbf{u}}^1 ) = ({\mathbf{Au}}^0, {\mathbf{u}}^0 ) = ({\mathbf{A}} {\varphi}, {\varphi}). $

Это равенство может быть выполнено лишь в случае

$ \left({\left({{\mathbf{B}} - \frac{\tau}{2}{\mathbf{A}}}\right){\mathbf{w}\mathbf{w}}, {\mathbf{w}}}\right) > 0. $

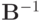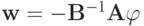В силу того, что {\mathbf{B}} = {\mathbf{B}}^* > 0, существует {\mathbf{B}}^{- 1}. Так как \varphi - произвольный элемент нашего пространства сеточных функций , то {\mathbf{w}} = {- {\mathbf{B}}^{- 1}{\mathbf{A}} \varphi} — произволен. Последнее равенство выполнено при любых 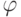$ \varphi $, значит

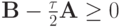
$ {\mathbf{B}} - \frac{\tau}{2}{\mathbf{A}} \ge 0 $
. Теорема доказана.

Теорема 4. Пусть \mathbf{A , B} — постоянные самосопряженные положительные операторы. Тогда условие

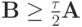
$ {\mathbf{B}} \ge \frac{\tau}{2}{\mathbf{A}} $
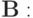
необходимо и достаточно для устойчивости по начальным данным в энергетической норме, порождаемой оператором \mathbf{B}:

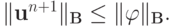
\|{\mathbf{u}}^{n + 1}\|_{\mathbf{B}} \le \| {\varphi}\|_{\mathbf{B}}.

Таким образом, получим следующее правило исследования устойчивости двухслойных разностных схем.

  1. Приводим схему к каноничному виду.
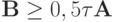  2. Исследуем свойства оператора \mathbf{A}. Если он является положительным, самосопряженным и независящим от n, проверяется условие {\mathbf{B}} \ge 0, 5{\tau}{\mathbf{A}}.

Рассмотрим теперь устойчивость схемы Кранка - Николсон для уравнения теплопроводности. Эта схема введена в рассмотрение в начале данного параграфа. В операторном виде она записывается так:

$ \frac{{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n}}}{\tau} = - \frac{1}{2}{\mathbf{Au}}^{n} - \frac{1}{2}{\mathbf{Au}}^{n + 1}. $

Запишем ее в каноническом виде:

$ \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{A}}}\right) \frac{{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n}}}{\tau} = - {\mathbf{Au}}^{n}. $
Дальше >>
Лекция 1: 1234567891011 || Лекция 2 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 30
Максим Радунцев
Максим Радунцев
Россия
предложить дружбу
Надежда Павленко
Надежда Павленко
Россия, Ставрополь
предложить дружбу