Численные методы решения уравнений в частных производных

:

Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Уровень: профессионал | Доступ: платный

Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость

A
|
версия для печати
Лекция 1: 1234567891011 || Лекция 2 >

По доказанной ранее теореме, данная схема устойчива по начальным данным в 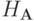H_{\mathbf{A}} в случае, если

$ {\mathbf{B}} = {\mathbf{E}} + \frac{\tau}{2}{\mathbf{A}} \ge \frac{\tau}{2}{\mathbf{A}} \Rightarrow {\mathbf{E}} > 0 \quad \mbox{(что всегда верно)}. $

Тогда, в энергетической норме, порождаемой оператором \mathbf{A}, схема Кранка - Николсон безусловно устойчива.

Схема с весами. Можно действовать также, как и для схемы Кранка - Николсон , а можно несколько иначе. Для общей записи схемы с весами

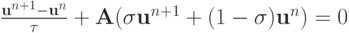
$ \frac{\mathbf{u}^{n + 1} - \mathbf{u}^{n}}{\tau} + \mathbf{A}({\sigma}\mathbf{u}^{n + 1} + (1 - \sigma)\mathbf{u}^{n}) = 0 $

иногда употребляется сокращенная форма

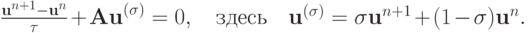
$ \frac{{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n}}}{\tau} + {\mathbf{Au}}^{({\sigma})} = 0, \quad \mbox{здесь} \quad {\mathbf{u}}^{({\sigma})} = {\sigma}{\mathbf{u}}^{n + 1} + (1 - {\sigma}){\mathbf{u}}^{n}. $

Умножив это разностное уравнение на 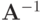{\mathbf{A}}^{- 1} слева, получаем:

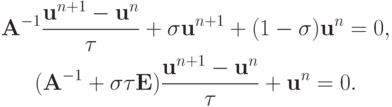
\begin{gather*} {\mathbf{A}}^{- 1} \frac{{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n}}}{\tau} + {\sigma}{\mathbf{u}}^{n + 1} + (1 - \sigma){\mathbf{u}}^{n} = 0, \\ ({\mathbf{A}}^{- 1} + {\sigma}{\tau}{\mathbf{E}}) \frac{{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n}}}{\tau} + {\mathbf{u}}^{n} = 0. \end{gather*}

Тогда необходимое и достаточное условие устойчивости в норме, порождаемой оператором 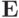\mathbf{E} (т.е. в евклидовой норме)

$ ({\mathbf{A}}^{- 1} + {\sigma}{\tau}{\mathbf{E}}) \ge \frac{\tau}{2}{\mathbf{E}}, {\mathbf{A}}^{- 1} + \left({{\sigma}- \frac{1}{2}}\right){\tau}\mathbf{E}} \ge 0. $

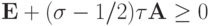Так как {\mathbf{A}} = {\mathbf{A}}^* > 0, домножим обе части последнего неравенства на \mathbf{A}, тогда {\mathbf{E}} + ({\sigma}- 1/2){\tau}{\mathbf{A}} \ge 0 — условие устойчивости схемы с весами.

Следствие. Неявная схема (\sigma = 1) безусловно устойчива в норме ||.|| = (., .)1/2 (аналог нормы L2 ).

Докажем теперь, что из равномерной устойчивости однородной разностной схемы следует устойчивость по правой части.

Рассмотрим уравнение

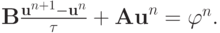
$ {\mathbf{B}} \frac{{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n}}}{\tau} + {\mathbf{Au}}^{n} = {\varphi}^{n}. $

Умножив это равенство скалярно на 2{\tau}{\mathbf{y}}_{\tau} = 2{\tau}\frac{{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n}}}{\tau}, $ получим

$ 2{\tau}\left({\left({{\mathbf{B}} - \frac{\tau}{2}{\mathbf{A}}}\right){\mathbf{y}}_{\tau}, {\mathbf{y}}_{\tau}}\right) + ({\mathbf{Au}}^{n + 1}, {\mathbf{u}}^{n + 1} ) = ({\mathbf{Au}}^{n}, {\mathbf{u}}^{n} ) + 2{\tau}({\varphi}^{n}, {\mathbf{y}}_{\tau} ) $

(это — энергетическое множество для неоднородного уравнения). Кроме того,

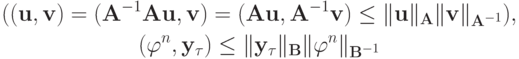
\begin{gather*} (({\mathbf{u}}, {\mathbf{v}}) = ({\mathbf{A}}^{- 1}{\mathbf{Au}}, {\mathbf{v}}) = ({\mathbf{Au}}, {\mathbf{A}}^{- 1}{\mathbf{v}}) \le \|{\mathbf{u}}\|_{\mathbf{A}} \|{\mathbf{v}}\|_{{\mathbf{A}}^{- 1}}), \\ ({\varphi}^{n}, {\mathbf{y}}_{\tau} ) \le \|{\mathbf{y}}_{\tau}\|_{\mathbf{B}}\| {\varphi}^{n}\|_{{\mathbf{B}}^{- 1}} \end{gather*}

(аналог неравенства Коши - Буняковского).

Теперь используем \varepsilon - неравенство

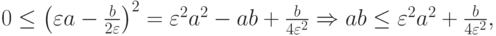
$ 0 \le \left({\varepsilon a - \frac{b}{2 \varepsilon }}\right)^2 = {\varepsilon}^2 a^2 - {ab} + \frac{b}{4{\varepsilon}^2} \Rightarrow {ab} \le {\varepsilon}^2 a^2 + \frac{b}{4{\varepsilon}^2}, $

тогда получаем

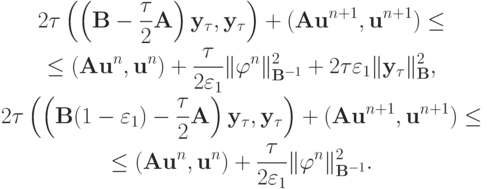
\begin{gather*} 2{\tau}\left({\left({{\mathbf{B}} - \frac{\tau}{2}{\mathbf{A}}}\right){\mathbf{y}}_{\tau}, {\mathbf{y}}_{\tau}}\right) + ({\mathbf{Au}}^{n + 1}, {\mathbf{u}}^{n + 1} ) \le \\ \le ({\mathbf{Au}}^{n}, {\mathbf{u}}^{n} ) + \frac{\tau}{{2 \varepsilon_1}}\| {\varphi}^{n}\|_{{\mathbf{B}}^{- 1}}^2 + 2{\tau}\varepsilon_1 \|{\mathbf{y}}_{\tau}\|_{\mathbf{B}}^2 , \\ 2{\tau}\left({\left({{\mathbf{B}}(1 - \varepsilon_1 ) - \frac{\tau}{2}{\mathbf{A}}}\right) {\mathbf{y}}_{\tau}, {\mathbf{y}}_{\tau}}\right) + ({\mathbf{Au}}^{n + 1}, {\mathbf{u}}^{n + 1} ) \le \\ \le({\mathbf{Au}}^{n}, {\mathbf{u}}^{n} ) + \frac{\tau}{{2 \varepsilon_1}}\| {\varphi}^{n}\|_{{\mathbf{B}}^{- 1}}^2 . \end{gather*}

Выбираем \varepsilon:

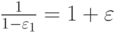
$ \frac{1}{1 - \varepsilon_1} = 1 + \varepsilon $
, тогда можно написать

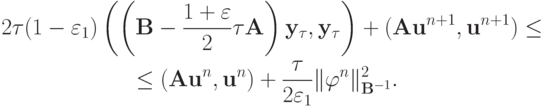
\begin{gather*} 2{\tau}(1 - \varepsilon_1 ) \left({\left({{\mathbf{B}} - \frac{{1 + \varepsilon }}{2}{\tau}{\mathbf{A}}}\right){\mathbf{y}}_{\tau}, {\mathbf{y}}_{\tau}}\right) + ({\mathbf{Au}}^{n + 1}, {\mathbf{u}}^{n + 1} ) \le \\ \le({\mathbf{Au}}^{n}, {\mathbf{u}}^{n} ) + \frac{\tau}{{2 \varepsilon_1}}\| {\varphi}^{n} \|_{{\mathbf{B}}^{- 1}}^2 . \end{gather*}

Пусть

$ {\mathbf{B}} - \frac{{1 + \varepsilon }}{2}{\tau}{\mathbf{A}} \ge 0, \varepsilon > 0, \varepsilon $
не зависит от сеточных параметров

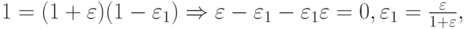
$ 1 = (1 + \varepsilon )(1 - \varepsilon_1 ) \Rightarrow \varepsilon - \varepsilon_1 - \varepsilon_1 \varepsilon = 0, \varepsilon_1 = \frac{\varepsilon }{{1 + \varepsilon }}, $

получаем

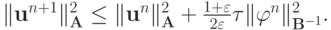
$ \|{\mathbf{u}}^{n + 1}\|_{\mathbf{A}}^2 \le \|{\mathbf{u}}^{n}\|_{\mathbf{A}}^2 + \frac{{1 + \varepsilon }}{{2 \varepsilon }}{\tau}\|{\varphi}^{n}\|_{{\mathbf{B}}^{- 1}}^2 . $

Откуда сразу следует

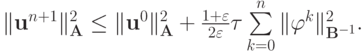$ {\|{\mathbf{u}}^{n + 1}\|_{\mathbf{A}}^2 \le \|{\mathbf{u}}^0\|_{\mathbf{A}}^2 + \frac{{1 + \varepsilon }}{{2 \varepsilon }}{\tau}\sum\limits_{k = 0}^{n}{\|{\varphi}^{k}\|_{{\mathbf{B}}^{- 1}}^2}.} $ ( 1.9)

Таким образом, для неоднородной разностной схемы доказана следующая теорема.

Теорема. Для разностной схемы вида

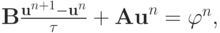
$ {\mathbf{B}} \frac{{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n}}}{\tau} + {\mathbf{Au}}^{n} = {\varphi}^{n}, $

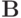где \mathbf{A} — постоянный (т.е. не зависящий явно от n ) положительно определенный самосопряженный оператор, а \mathbf{B} удовлетворяет условию

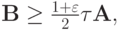
$ {\mathbf{B}} \ge \frac{1 + \varepsilon }{2}{\tau}{\mathbf{A}}, $

где 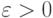\varepsilon > 0 не зависит от сеточных параметров , выполнена априорная оценка (1.9).

Вообще, в силу того, что разностная схема устойчива по начальным данным при {\mathbf{B}} = {\mathbf{B}}^* > 0, из равномерной устойчивости по начальным данным следует устойчивость по правой части.

Так как {\mathbf{B}} = {\mathbf{B}}^* > 0, то {\exists}{\mathbf{B}}^{- 1}, тогда

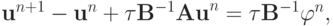
{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n} +{\tau}{\mathbf{B}}^{- 1}{\mathbf{Au}}^{n} ={\tau}{\mathbf{B}}^{- 1} {\varphi}^{n},

или

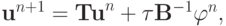
{\mathbf{u}}^{n + 1} = {\mathbf{Tu}}^{n} +{\tau}{\mathbf{B}}^{- 1} {\varphi}^{n},

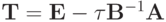где {\mathbf{T}} = {\mathbf{E}} -{\tau}{\mathbf{B}}^{- 1}{\mathbf{A}} — оператор послойного перехода.

Равномерная устойчивость по начальным данным означает, что 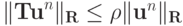\|{\mathbf{Tu}}^{n}\|_{\mathbf{R}} \le {\rho}\|{\mathbf{u}}^{n}\|_{\mathbf{R}}. Тогда из предыдущего равенства с использованием неравенства треугольника получим

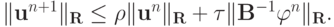
\|{\mathbf{u}}^{n + 1}\|_{\mathbf{R}} \le {\rho}\|{\mathbf{u}}^{n}\|_{\mathbf{R}} + {\tau}\|{\mathbf{B}}^{- 1} {\varphi}^{n}\|_{\mathbf{R}}.

Применяя оценку n раз , получим априорную оценку для устойчивости по правой части с использованием энергетической нормы, порождаемой оператором {\mathbf{R}} = {\mathbf{R}}^* > 0:

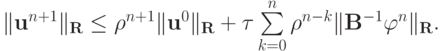
\|{\mathbf{u}}^{n + 1}\|_{\mathbf{R}} \le {\rho}^{n + 1}\|{\mathbf{u}}^0 \|_{\mathbf{R}} +{\tau}\sum\limits_{k = 0}^{n}{{\rho}^{n - k}\|{\mathbf{B}}^{- 1} {\varphi}^{n}\|_{\mathbf{R}}}.

Теперь попробуем обобщить полученные результаты на случай операторов , зависящих от времени.

Для начала рассмотрим аппроксимацию типа Кранка - Николсона

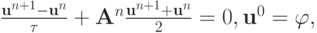
$ \frac{{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n}}}{\tau} + {\mathbf{A}}^{n} \frac{{{\mathbf{u}}^{n + 1} + {\mathbf{u}}^{n}}}{2} = 0, {\mathbf{u}}^0 = \varphi , $

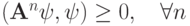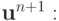
при этом ({\mathbf{A}}^{n}{{{\psi}}}, {{{\psi}}}) \ge 0, \quad {\forall}n. Самый простой способ рассмотрения этого уравнения — разрешить его (в операторном виде) относительно {\mathbf{u}}^{n + 1}:

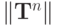$ {\mathbf{u}}^{n + 1} = \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{A}}^{n}}\right)^{- 1} \left({{\mathbf{E}} - \frac{\tau}{2}{\mathbf{A}}^{n}}\right){\mathbf{u}}^{n} = {\mathbf{T}}^{n}{\mathbf{u}}^{n}. $

Оценим \|{\mathbf{T}}^{n}\|. Воспользуемся тем, что

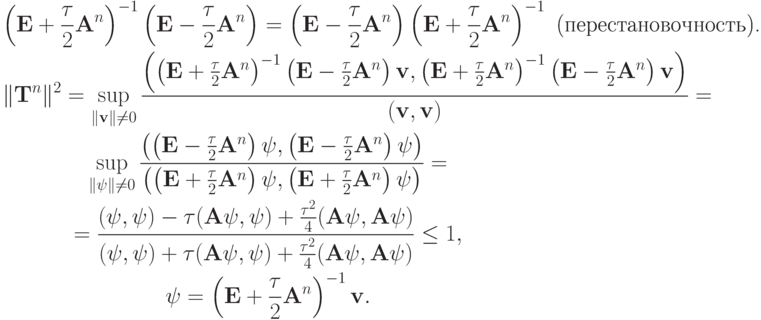
\begin{gather*} \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{A}}^{n}}\right)^{- 1} \left({{\mathbf{E}} - \frac{\tau}{2}{\mathbf{A}}^{n}}\right) = \left({{\mathbf{E}} - \frac{\tau}{2} {\mathbf{A}}^{n}}\right) \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{A}}^{n}}\right)^{- 1} \mbox{ (перестановочность).} \\ \|{\mathbf{T}}^{n}\|^2 = \sup\limits_{\|{\mathbf{v}}\| \ne 0} \frac{{\left({\left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{A}}^{n}}\right)^{- 1} \left({{\mathbf{E}} - \frac{\tau}{2}{\mathbf{A}}^{n}}\right){\mathbf{v}}, \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{A}}^{n}}\right)^{- 1} \left({{\mathbf{E}} - \frac{\tau}{2}{\mathbf{A}}^{n}}\right){\mathbf{v}}}\right)}}{{({\mathbf{v}}, {\mathbf{v}})}} = \\ \sup\limits_{\|{{{\psi}}}\| \ne 0} \frac{{\left({\left({{\mathbf{E}} - \frac{\tau}{2}{\mathbf{A}}^{n}}\right){{{\psi}}}, \left({{\mathbf{E}} - \frac{\tau}{2} {\mathbf{A}}^{n}}\right){{{\psi}}}}\right)}}{{\left({\left({{\mathbf{E}} + \frac{\tau}{2} {\mathbf{A}}^{n}}\right){{{\psi}}}, \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{A}}^{n}}\right){{{\psi}}}}\right)}} = \\ = \frac{{({{\psi}}, {{{\psi}}}) -{\tau}({\mathbf{A \psi}}, {{{\psi}}}) + \frac{{{\tau}^2}}{4}({\mathbf{A \psi}}, {\mathbf{A \psi}})}}{{({{{\psi}}}, {{{\psi}}}) +{\tau}({\mathbf{A \psi}}, {{{\psi}}}) + \frac{{{\tau}^2}}{4}({\mathbf{A \psi}}, {\mathbf{A \psi}})}} \le 1 , \\ {{{\psi}}} = \left({{\mathbf{E}} + \frac{\tau}{2}{\mathbf{A}}^{n}}\right)^{- 1} {\mathbf{v}}. \end{gather*}

Факт, что \|({\mathbf{E}} - {\sigma}{\mathbf{A}})({\mathbf{E}} + {\sigma}{\mathbf{A}})^{- 1}\| \le 1 , \quad {\forall}{\sigma} > 0, {\mathbf{A}} = {\mathbf{A}}^* > 0, носит название леммы Келлога.

Для сеточной функции используем норму \|{\mathbf{v}}\| = ({\mathbf{v}}, {\mathbf{v}})^{1/2}. Подобный результат уже был получен при постоянном (не зависящем от времени) \mathbf{A}.

Везде в доказательствах существенную роль играет то, что 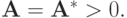{\mathbf{A} = \mathbf{A}^* > 0.} Может получиться так, что {\mathbf{A}} > 0, но {\mathbf{A}} \ne {\mathbf{A}}^*:

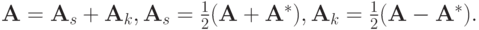
$ {\mathbf{A}} = {\mathbf{A}}_{s} + {\mathbf{A}}_k, {\mathbf{A}}_{s} = \frac{1}{2}({\mathbf{A}} + {\mathbf{A}}^* ), {\mathbf{A}}_k = \frac{1}{2}({\mathbf{A}} - {\mathbf{A}}^* ). $

В этом случае многие свойства разностных схем аналогичны доказанным выше.

Может быть так, что 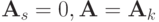{\mathbf{A}}_{s} = 0, {\mathbf{A}} = {\mathbf{A}}_k. Тогда

({\mathbf{Av}}, {\mathbf{v}}) = - ({\mathbf{Av}}, {\mathbf{v}}) = 0

в силу кососимметричности оператора \mathbf{A}. Например:

\begin{gather*} \frac{{{\mathbf{u}}_m^{n + 1} - {\mathbf{u}}_m^{n}}}{\tau} + \frac{{{\mathbf{u}}_{m + 1}^{n} - {\mathbf{u}}_{m - 1}^{n}}}{{2h}} = 0. \\ {\mathbf{A}} = \left( \begin{array}{ccc} 0 & 1 & 0 \\ {- 1} & 0 & 1 \\ 0 & {- 1} & 0 \\ \end{array} \right), \quad {\mathbf{A}} = {\mathbf{A}}_k , \quad ({\mathbf{Av}}, {\mathbf{v}}) = 0 \quad {\forall}{\mathbf{v}}. \end{gather*}
Дальше >>
Лекция 1: 1234567891011 || Лекция 2 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 30
Максим Радунцев
Максим Радунцев
Россия
предложить дружбу
Надежда Павленко
Надежда Павленко
Россия, Ставрополь
предложить дружбу