Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений

Искажение сигнала и борьба с этим эффектом

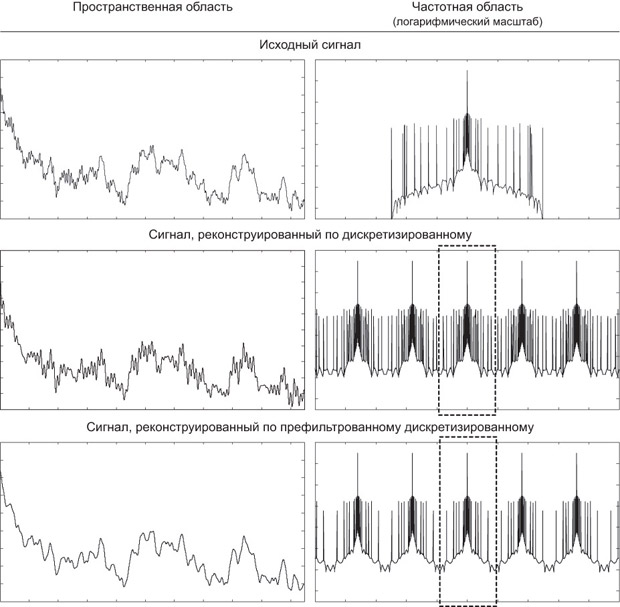
Как было показано при доказательстве теоремы Найквиста-Котельникова, при недостаточной частоте дискретизации восстановленный сигнал будет искажен. Это наглядно можно наблюдать в частотной области (см. рис. 7.6), т.к. при этом копии частотного спектра исходного сигнала будут суммироваться в пересекающихся областях, что даст мнимое увеличение веса компонент с этими частотами в спектре, некую подмену высокочастотных компонент низкочастотными, эффект, известный как алиасинг (англ. aliasing). Особенно наглядно этот эффект можно наблюдать на резких контрастных изменениях яркости (см., например, изображение на рис. 7.7). Этот эффект легко объясним, если рассмотреть прямоугольный сигнал и его Фурье-образ ( sinc ), который имеет спектр бесконечной ширины (см. рис. 7.9, прямоугольный фильтр).

Для борьбы с подобными явлениями применяют префильтрацию - свертку с некой функцией фильтра (о фильтрации в общем случае см. соответствующую "Фильтрация изображений" ), что эквивалентно умножению на Фурье-образ функции-фильтра в частотной области, перед тем как производится дискретизация. Цель префильтрации - заранее отсечь высокочастотные компоненты, которые могут привести к алиасингу. В идеале, для этого следовало бы применять функцию sinc (см. формулу (7.7), рис. 7.8), действие которой как раз и состоит в отсечении высоких частот, но она имеет бесконечный носитель^{1Носитель функции - максимальная область, в которой она принимает значения отличные от 0.}, что затрудняет ее применение в пространственной области. На практике используются различные аппроксимации с ограниченным носителем (см. таблицу 7.1 и рис. 7.9 и 7.10). Гауссовский фильтр обычно применяется с (так он лучше всего приближает sinc в частотной области), R берется порядка 2-3. У кубического фильтра присутствует параметр , с помощью которого можно регулировать степень размытия (увеличение a ) или, наоборот, более четкой передачи краев несмотря на некоторый алиасинг (уменьшение a ), стандарным компромиссным значением является a = -1. Для Lanzcos, который представляет собой обрезанный и сглаженный sinc, радиус R обычно равен 2 (так называемый Lanzcos2 ), реже - до 4. Большие значения не используются ввиду того, что носитель, а значит, и область интегрирования при свертке, будет слишком большой.

Понятно, что для дискретизации достаточно знать значения префильтрованной функции только в точках дискретизации. Это замечание служит основой для рассуждений в следующих разделах.

Рис. 7.6. Эффект алиасинга при недостаточной частоте дискретизации.

В двумерном случае фильтрация описывается следующим образом: интенсивность пикселя I(x, y) с центром в точке (x, y) будет определяться формулой двумерной свертки

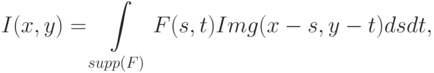( 7.8)

где F(s, t) - функция фильтра с центром в 0, supp(F) - ее носитель (область, где она не равна 0 ), Img(x, y) - непрерывное аналоговое изображение.

Рис. 7.7. Видимый эффект алиасинга на изображении: слева - исходное изображение без антиалиасинга, справа - с антиалиасингом. (Изображения получены с помощью POV-Ray.)

Рис. 7.8. Функция-фильтр Sinc.