Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений
Этот раздел посвящен проблемам представления непрерывного двумерного цветового сигнала, которым является изображение, на дискретной растровой сетке. Процесс получения дискретной аппроксимации непрерывного сигнала называется дискретизацией (англ. sampling). Сначала рассматривается общая теория, а затем приложения к обработке изображений.
7.1. Дискретизация. Теорема Найквиста-Котельникова
Общий процесс работы с изображением в компьютере представлен на рис. 7.1. Изображение в компьютере хранится в дискретном виде. Для получения такого дискретного представления из непрерывных аналоговых изображений реального мира (как мы их видим глазами или через оптические устройства) и применяется дискретизация. Фактически ее осуществляют устройства ввода, такие как цифровой фотоаппарат, сканер или другие ( "Современные аппаратные средства растровой графики" ). Затем с полученным дискретным изображением могут производиться различные преобразования, в том числе рассмотренные далее в данной лекции. И в результате оно отображается на устройстве вывода, таком как, например, ЭЛТ-дисплей. Дисплей фактически осуществляет реконструкцию аналогового изображения по его дискретизированному представлению. Насколько точно можно провести такую реконструкцию и от чего это зависит, и обсуждается далее.
Наиболее корректно рассматривать возникающие проблемы в рамках теории обработки сигналов (англ. signal processing). Двумерное изображение можно представлять как двумерный сигнал, рассматривая его как отображение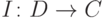 
, где C - атрибут изображения, - интенсивность ( C - отрезок) или цвет; в последнем случае чаще всего C - RGB-куб (
"Основные понятия. Представление цвета в машинной графике"
). В аналоговой форме этот сигнал непрерывный (определенный на прямоугольнике D ), а в дискретной - определенный лишь на точках растра D. В дальнейшем рассмотрении дискретный случай представляется как функция, отличная от нуля только в точках
растра (см. точечное толкование понятия растра в
"Основные понятия. Представление цвета в машинной графике"
). Теория обработки сигналов рассматривает периодические сигналы, определенные на всем континууме ( 
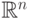). Поэтому для рассмотрения изображений, определенных на прямоугольнике, поступают двояко: либо трактуют как сигнал, равный 0 везде кроме данного прямоугольника, либо считают длину и ширину периодами и производят "замощение" всей плоскости сдвинутыми на периоды копиями изображения. Последний случай используется чаще.
Далее для упрощения рассуждений мы будем рассматривать одномерные сигналы с одномерной областью определения. Для наглядности на рис. 7.2 представлен одномерный сигнал как срез двумерного изображения.
Сигналы рассматривают как в пространственной области (англ. spatial domain) - это обычная область определения (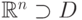 
), так и в частотной области (англ. frequency domain), которая получается как область определения коэффициентов разложения сигнала по тригонометрической системе Фурье. Частотная область представляет из себя 
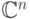. Частотное представление F(f) для одномерной функции I(x) рассчитывается при помощи преобразования Фурье:
![F(f) = \int_{-\infty}^{\infty} I(x)[\cos 2\pi fx - i \sin 2\pi fx]dx.](/sites/default/files/tex_cache/379e3abb10782cbee8b894232f9c3177.png) |
( 7.1) |
Если представить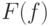 
в виде 
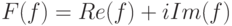, то модуль, или амплитуда, - это 
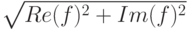, а фазовый сдвиг, или фазовый угол, - ![\arctan [\frac{Im(f)}{Re(f) }]](/sites/default/files/tex_cache/436049fff1c40c43c5ebd4f3ef59e230.png)
. На графиках далее будут представлены только более наглядные значения амплитуды. В многомерном случае произведение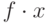 
заменяется на скалярное произведение векторов 
и 
. Для интересующего нас двумерного случая преобразование Фурье запишется как
![F(f_x, f_y) = \int_{\mathbb{R}^2}^{} I(x, y)[\cos (2\pi(f_xx + f_yy)) - i \sin (2\pi(f_xx + f_yy))]dxdy.](/sites/default/files/tex_cache/76af6f70b992600a5bfece081169e8c3.png) |
( 7.2) |
Далее для упрощения рассуждения будут проводиться в одномерном случае, впрочем, их несложно обобщить на общий 
-мерный случай. Обратно к пространственной области можно перейти с помощью обратного преобразования Фурье:
![I(x) = \int_{-\infty}^{\infty} F(f)[\cos 2\pi fx + i \sin 2\pi fx]df.](/sites/default/files/tex_cache/5b1056046fb5fa715ae27f5bcfa23148.png) |
( 7.3) |
В дискретном случае, если сигнал представлен в виде функции, определенной на 
точках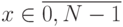 
, используется дискретное преобразование Фурье (ДПФ), которое по сути является дискретизацией непрерывного преобразования Фурье, примененного к дискретному сигналу:
![F(f) =\sum\limits_{x=0}^{N-1}I(x) \left[ \cos \frac{2\pi fx}{N} - i \sin \frac{2\pi fx}{N}\right],](/sites/default/files/tex_cache/5375110b5c9fe77bc6498a4778e481df.png) |
( 7.4) |
где 
также дискретна. Соответствующее обратное дискретное преобразование Фурье дается формулой
![I(x) = \frac{1}{N}\sum\limits_{x=0}^{N-1}F(f) \left[ \cos \frac{2\pi fx}{N} + i \sin \frac{2\pi fx}{N}\right],](/sites/default/files/tex_cache/e0fa5932a5d40a4d16ac16b53f624967.png) |
( 7.5) |
где 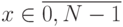. Прямое и обратное дискретные преобразования Фурье по формулам (7.4), (7.5) вычисляются за O(N2). Существуют алгоритмы т.н. Быстрого преобразования Фурье, работающие за O(N logN) (см. [1], [42]). Если в частотной области F(f) = 0, |f| > fH, то говорят, что сигнал (функция) I(x) имеет ограниченный спектр с максимальной частотой fH. Иными словами, в разложении функции по тригонометрической системе не присутствуют тригонометрические функции с частотой более fH.
Обычно дискретизация происходит путем измерения сигнала (взятия значения функции) через равные промежутки в области определения. Эта операция математически описывается как умножение функции I(x) на гребенчатый фильтр, состоящий из последовательности равномерно сдвинутых функций Дирака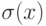 
:
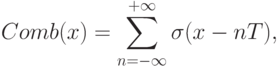
где T = 1/fs - период, а fs - частота дискретизации (см. рис. 7.3). Интересным свойством функции Comb является то, что ее преобразование Фурье также есть функция Comb, но с другими амплитудой (не 1, а fs ) и частотой (также fs ).