Основные понятия. Представление цвета в машинной графике
1.1. Растровая и векторная графика. Понятие растра
Для представления графической информации на двумерной плоскости (например, экране монитора, странице книги и т.п.) в вычислительной технике применяются два основных подхода: растровый и векторный1Аналогичные концепции есть и в трехмерной графике, но это выходит за рамки предмета данного курса..
При векторном подходе графическая информация описывается как совокупность неких абстрактных геометрических объектов, таких как прямые, отрезки, кривые, прямоугольники и т.п.
Растровая графика же оперирует изображениями в виде растров. Неформально можно сказать, что растр - это описание изображения на плоскости путем разбиения всей плоскости или ее части на одинаковые квадраты и присвоение каждому квадрату своего цветового (или иного, например, прозрачности, для последующего наложения изображений друг на друга) атрибута. Если таких квадратов имеется конечное число, то получается, что непрерывная цветовая функция изображения приближенно представлена конечной совокупностью значений атрибутов. Иногда понятие растра определяют более широко: как разбиение плоскости (или ее участка) на равные элементы (т.е."замощение"), например шестиугольниками ( гексагональный растр). Далее в этом курсе расширенное толкование использоваться не будет.
С другой стороны, растр можно рассматривать как кусочно-постоянную аппроксимацию изображения, заданного как цветовая функция на плоскости. Такая точка зрения позволяет применять математический аппарат теории аппроксимации для работы с растровыми изображениями, о чем подробнее будет рассказано далее.
Формально, введем следующие определения:
Растр (англ. raster) - отображение вида

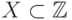 ,
,  ,
,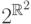 обозначает множество всех подмножеств
обозначает множество всех подмножеств  ,
,
C - множество значений атрибутов (как правило, цвет).
f(i, j) - элемент растра, называемый пикселем (англ. pixel (от picture element)), в русскоязычной литературе иногда также переводится как пиксел);
f(i, j) = (A(i, j),C(i, j)), где
-
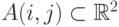 - область пикселя,
- область пикселя, -
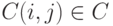 - атрибут пикселя (как правило, цвет). Чаще всего мы будем пользоваться следующими двумя видами атрибутов:
- атрибут пикселя (как правило, цвет). Чаще всего мы будем пользоваться следующими двумя видами атрибутов:- C(i, j) = I(i, j) - интенсивность (или яркость) пикселя;
- C(i, j) = {R(i, j),G(i, j),B(i, j)} - цветовые атрибуты в цветовой модели RGB (см. раздел 1.2).
Также иногда будут употребляться матричные обозначения:
Mij = (Aij ,Cij)
Aij может определяться двояко, в зависимости от того, с какой моделью мы хотим работать:
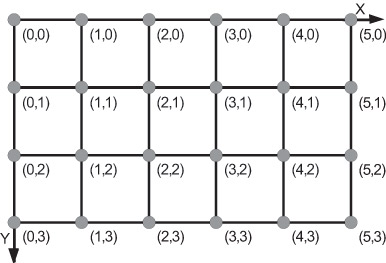
- Aij := (i, j) - одна точка. Пример такой модели растра см. на рис. 1.1;
-
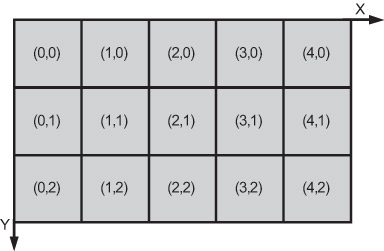
 - квадрат. Пример такой модели растра см. на рис. 1.2. На реальных графических устройствах физически пиксели могут быть прямоугольниками, что иногда порождает дополнительные трудности.
- квадрат. Пример такой модели растра см. на рис. 1.2. На реальных графических устройствах физически пиксели могут быть прямоугольниками, что иногда порождает дополнительные трудности.
В реальности, как правило, X и Y - ограниченные наборы неотрицательных целых чисел; такой растр называется прямоугольным. Для него применимо понятие Аспектовое отношение (англ. aspect ratio) - отношение ширины к высоте растра (|X|/|Y|). Чаще всего такое понятие употребляется в связи с физическими растрами (дисплеями, ПЗС-матрицами фотоаппаратов и т.д.) и записывается в виде простой дроби с ":", например "4:3".
Бесконечные растры (когда X и Y неограниченны) бывают удобны для описания алгоритмов, позволяя избежать особых ситуаций. Впрочем, самой сутью некоторых алгоритмов является как раз работа с граничными случаями.
Растровое представление является естественным в тех случаях, когда нам не известна дополнительная информация об изображаемых объектах (например, цифровым фотоаппаратом можно снимать изображения произвольного содержания). В случае же векторного описания примитивами являются более сложные объекты (линии и области, ограниченные линиями), что предполагает априорные знания о структуре изображения. В последнее время проявляется ярко выраженная тенденция к преобладанию устройств ввода-вывода двумерной графической информации, основанных на растровом принципе как более универсальном. Возникающая при выводе задача отображения геометрических объектов, заданных их математическим описанием (например, координатами концевых точек и цветом для отрезка), на растре, называемая растеризацией, рассмотрена в последующих разделах.
При построении алгоритмов, работающих с изображениями, можно также пользоваться информацией как непосредственно атрибутов пикселей, так и работать с примитивами более высокого порядка. В данном курсе в основном рассматриваются алгоритмы первого типа, про которые говорят, что они работают в пространстве изображения (англ. image space), тогда как вторые работают в объектном пространстве (англ. object space) (эти термины чаще употребляются в трехмерной графике).
Устройства отображения растровой графики рассматриваются в следующей лекции.