Алгоритмы растеризации отрезков, окружностей и эллипсов

Этот раздел посвящен растеризации простейших геометрических объектов, таких как отрезки, окружности и эллипсы, на плоскости.

3.1. Введение в растеризацию кривых

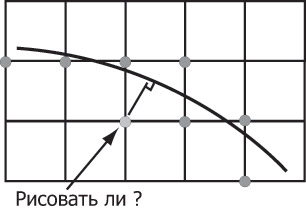
Пусть у нас есть некоторая кривая, и мы хотим построить ее изображение на растровой решетке. Возникает вопрос: какие из ближайших пикселей следует закрашивать? В данной и следующей лекциях мы рассмотрим случай построения на монохромном растре, когда возможны только два уровня интенсивности закраски пикселя - "полностью закрашен" или "полностью не закрашен". Если же допустимы несколько уровней интенсивности, то можно растеризовывать более аккуратно, уменьшая эффекты алиасинга (т.е. ступенчатости), "Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений" .

Рис. 3.1. Изображение кривых на растре.

Пусть (x₀, y₀) - фиксированный пиксель, а (x, y) - некоторый другой пиксель на плоскости. Тогда для определения их близости вводятся следующие понятия:

1. 4-связность |x-x0|+|y-y0|=1
2. 8-связность max{|x-x0|, |y-y0|}=1

В дальнейших рассуждениях расстояние будем считать заданным стандартной евклидовой метрикой^{1 dist(P₁,P₂) = ((x₁ - x₂)2 + (y₁ - y₂)2)1/2} .

3.2. Изображение отрезка с целочисленными координатами концов

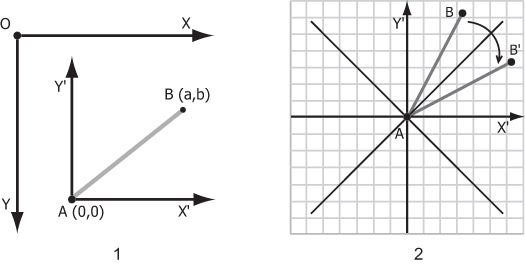
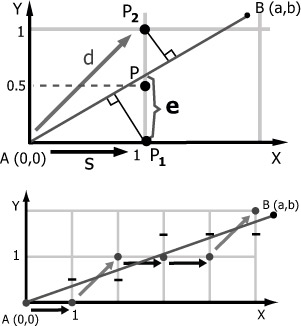
Пусть наш отрезок - это AB. Перейдем от системы координат Oxy к Ax'y' (см. рис. 3.2, этап 1). Отрезок может лежать в любом из 8 октантов, но всегда существуют симметрии относительно осей, разделяющих эти октанты, симметрии определяются матрицами

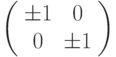
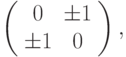
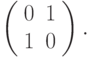
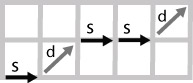
• s - горизонтальное смещение;
• d - диагональное смещение.

Рис. 3.2. Переход к каноническому случаю в два этапа.

Эквивалентно этой последовательности можно сопоставить бинарный код, где 0 соответствует s, а 1 соответствует d. Такой код для рисования отрезка 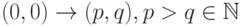называется кодом Ротштейна [46] для .

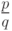Пусть plot(x,y) - функция, закрашивающая точку растра с координатами (x,y).

Рис. 3.3. Кодирование закрашивания отрезка (или код Ротштейна).

Цифровой дифференциальный анализатор

Алгоритм Цифровой дифференциальный анализатор (англ. DDA - Digital Differential Analyzer) строит 8-связную линию.

Для начала, пусть P₁ = (1, 0) ; P₂ = (1, 1). Для определения того, какой из пикселей, - P₁ или P₂, - следует закрасить, сравним расстояния до них. В силу подобия треугольников, образованных пересечением рисуемого отрезка, прямой x = 1 и перпендикулярами из P₁ и P₂ на отрезок (см. рис. 3.4), достаточно сравнить e (ординату пересечения отрезка c прямой x = 1 ) с . Далее, для следующего шага алгоритм работает аналогично с учетом изменения e - ординаты пересечения отрезка со следующей вертикальной прямой .

Рис. 3.4. Цифровой дифференциальный анализатор.

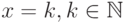// Координаты концов отрезка - (0,0) и (a,b)

e = b/a; // Текущая ордината
delta_e = b/a; // Приращение ординаты

// (x,y) - Координаты текущей точки
x = 0; y = 0;

while( x < a )
{
      plot(x, y);

      if( e > 1/2 )
      {
            // d : диагональное смещение
            x++; y++;

            // т.к. произошло смещение по y на 1 вверх
            e += delta_e - 1;
      }
      else
      {
            // s : горизонтальное смещение
            x++;
            e += delta_e;
      }
}

Недостатком данного алгоритма является то, что он работает с числами с плавающей точкой.