Фильтрация изображений
8.1. Введение
Представим себе, что, глядя на какую-нибудь сцену одним глазом, мы подносим к нему стеклянную пластину. Если эта пластина не была идеально прозрачной, то наблюдаемое изображение изменится. В зависимости от стекла, из которого сделана пластина, изменение может быть самым разнообразным. К примеру, если это стекло было цветным, то изображение приобретет соответствующий оттенок, а от мутного стекла - станет размытым.
Фильтрация изображений аналогична такому разглядыванию мира через стеклянную пластину, хотя и позволяет добиться гораздо большего разнообразия эффектов, чем эксперименты с разными пластинами. Под фильтрацией изображений понимают операцию, имеющую своим результатом изображение того же размера, полученное из исходного по некоторым правилам. Обычно интенсивность (цвет) каждого пикселя результирующего изображения обусловлена интенсивностями (цветами) пикселей, расположенных в некоторой его окрестности в исходном изображении.
Правила, задающие фильтрацию (их называют фильтрами ), могут быть самыми разнообразными. В этой лекции мы рассмотрим простейшие фильтры. Заметим, что, согласно предложенному определению, операция, заключающаяся в последовательном применении двух или более фильтраций, тоже является фильтрацией. Таким образом, можно говорить о составных фильтрах, соответствующих комбинациям простых. Изучив основные типы фильтров в данной лекции, мы будем иметь дело с применением фильтров, составленных из них, для решения разнообразных задач в последующих лекциях. Фильтрация изображений является одной из самых фундаментальных операций компьютерного зрения, распознавания образов и обработки изображений. Фактически, с той или иной фильтрации исходных изображений начинается работа подавляющего большинства методов. Рассматриваемые в этой лекции фильтры имеют, таким образом, чрезвычайную важность с точки зрения их применения в различных приложениях.
8.2. Линейные фильтры
Определение
Линейные фильтры представляют собой семейство фильтров, имеющих очень простое математическое описание. Вместе с тем они позволяют добиться самых разнообразных эффектов. Будем считать, что задано исходное полутоновое изображение A, и обозначим интенсивности его пикселей A(x, y). Линейный фильтр определяется вещественнозначной функцией F, заданной на растре. Данная функция называется ядром фильтра, а сама фильтрация производится при помощи операции дискретной свертки (взвешенного суммирования) (см. также "Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений" ):
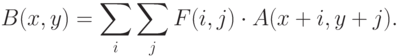 |
( 8.1) |
Результатом служит изображение B. В определении (8.1) мы опустили пределы суммирования. Обычно ядро фильтра отлично от нуля только в некоторой окрестности N точки (0, 0). За пределами этой окрестности F(i, j) или в точности равно нулю, или очень близко к нему, так что можно им пренебречь. Суммирование в (8.1)
производится по  , и значение каждого пикселя B(x, y) определяется пикселями изображения A, которые лежат в окне N, центрированном в точке (x, y) (мы будем обозначать это множество N(x, y) ). Ядро фильтра, заданное на прямоугольной окрестности N, может рассматриваться как матрица m на n, где длины сторон являются нечетными числами. При задании ядра матрицей Mkl, ее следует центрировать:
, и значение каждого пикселя B(x, y) определяется пикселями изображения A, которые лежат в окне N, центрированном в точке (x, y) (мы будем обозначать это множество N(x, y) ). Ядро фильтра, заданное на прямоугольной окрестности N, может рассматриваться как матрица m на n, где длины сторон являются нечетными числами. При задании ядра матрицей Mkl, ее следует центрировать:
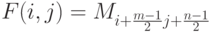 |
( 8.2) |
Также нуждается в дополнительном прояснении ситуация, когда пиксель (x, y) находится в окрестности краев изображения. В этом случае A(x + i, y + j) в определении (8.1) может соответствовать пикселю A, лежащему за пределами изображения A. Данную проблему можно разрешить несколькими способами.
- Не проводить фильтрацию для таких пикселей, обрезав изображение B по краям или закрасив их, к примеру, черным цветом.
- Не включать соответствующий пиксель в суммирование, распределив его вес F(i, j) равномерно среди других пикселей окрестности N(x, y).
- Доопределить значения пикселей за границами изображения при помощи экстраполяции. Например, считать постоянным значение интенсивности вблизи границы (для пикселя (-2, 5) имеем A(-2, 5) = A(0, 5) ) или считать постоянным градиент интенсивности вблизи границы ( A(-2, 5) = A(0, 5) + 2(A(0, 5) - A(1, 5)) ).
- Доопределить значения пикселей за границами изображения, при помощи зеркального отражения ( A(-2, 5) = A(2, 5) ).
Выбор конкретного способа нужно производить с учетом конкретного фильтра и особенностей конкретного приложения.
Разобрав общее определение линейных фильтров, перейдем к примерам.
