Фильтрация изображений
Разностные фильтры
В этом разделе мы кратко рассмотрим линейные фильтры, задаваемые дискретными аппроксимациями дифференциальных операторов (по методу конечных разностей ). Данные фильтры играют важнейшую роль во многих приложениях. В частности, нами будет подробно рассмотрено их применение для задачи поиска границ на изображении. В данном же разделе мы коротко рассмотрим их определения и свойства.
Простейшим дифференциальным оператором является взятие производной по x -координате 
. Данный оператор определен для непрерывных функций. Существует множество способов определить аналогичный оператор для дискретных изображений при помощи линейного фильтра. В частности, распространенными вариантами являются фильтры Прюита (Prewitt) и Собеля (Sobel).
Фильтр Прюита задается матрицей
 |
( 8.6) |
Фильтр Собеля задается матрицей
 |
( 8.7) |
Фильтры, приближающие оператор производной по y -координате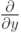 
, получаются путем транспонирования матриц.
В отличии от сглаживающих и контрастоповышающих фильтров, не меняющих среднюю интенсивность изображения (сумма элементов ядра равна единице), в результате применения разностных операторов получается, как правило, изображение со средним значением пикселя близким к нулю (сумма элементов ядра равна нулю). Вертикальным перепадам (границам) исходного изображения соответствуют пиксели с большими по модулю значениями на результирующем изображении. Поэтому разностные фильтры называют также фильтрами, находящими границы (рис. 8.4).
На верхнем рисунке - нахождение при помощи фильтра Собеля с ядром 
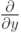, нижний - нахождение при помощи фильтра Собеля с ядром 
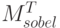. Серый цвет соответстует значению 0.
Аналогично вышеприведенным фильтрам, по методу конечных разностей можно составить фильтры для других дифференциальных операторов. В частности, важный для многих приложений дифференциальный оператор Лапласа ( лапласиан )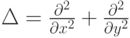 
можно приблизить для дискретных изображений фильтром с матрицей (один из вариантов):
 |
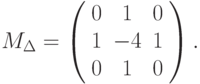( 8.8) |
Как видно на рис. 8.5, в результате применения дискретного лапласиана большие по модулю значения соответствуют как вертикальным, так и горизонтальным перепадам яркости. 
является, таким образом, фильтром, находящим границы любой ориентации. Нахождение границ на изображении может производиться путем применения этого фильтра и взятия всех
пикселей, модуль значения которых превосходит некоторый порог. Однако такой алгоритм имеет существенные недостатки. Главный из них - неопределенность в выборе величины порога. Для разных частей изображения приемлемый результат обычно получается при существенно разных пороговых значениях. Кроме того, разностные фильтры очень чувствительны к шумам изображения. Задача нахождения границ на изображении является, как мы видим, весьма непростой. Мы посвятим ей отдельную
"Нахождение границ"
.
Вверху- исходное изображение, внизу - результат применения фильтра 
. Серый цвет соответстует значению 0
Заметим, что выделение всех пикселей, значения которых по модулю больше некоторого порога, является некоторой нелинейной локальной операцией, которую можно рассматривать как простейший пример нелинейной фильтрации, к рассмотрению которой мы и переходим.