Сжатие изображений с потерями
14.1. Необходимость сжатия с потерями
Как указано в первом параграфе предыдущей лекции, объем информации, нужной для хранения изображений, обычно велик. При этом с каждым днем разрешающая способность устройств ввода изображений растет. Некоторое время назад стало очевидно, что классические алгоритмы не обеспечивают достаточной степени сжатия. Являясь алгоритмами общего назначения, они не учитывали того, что сжимаемая информация есть изображение. Соответственно, были разработаны алгоритмы, обеспечивающие сжатие с потерями информации, которые позволили существенно поднять степень компрессии.
Сжатие с потерями основывается на особенностях восприятия человеком изображения: наибольшей чувствительности в определенном диапазоне волн цвета, способности воспринимать изображение как единое целое, не замечая мелких искажений. Также используется тот факт, что изображение - двумерный объект. Главный класс изображений, на который ориентированы алгоритмы сжатия с потерями, - фотографии, изображения с плавными цветовыми переходами.
14.2. Оценка потерь
Напомним, что A называется алгоритмом сжатия c потерями (англ. lossy compression), если он не обеспечивает возможность точного восстановления исходного изображения. Т.е. подбирается пара A, A*, где A* приближенно восстанавливает изображение: для любого изображения I A(I) = I1, A*(I1) = I2 и при этом полученное восстановленное изображение I2 не обязательно точно совпадает с I (см. определение в первом параграфе предыдущей лекции). Возникает вопрос: как оценивать потери визуальной информации, т.е. меру отличия I от I2? Существует множество хороших мер для оценки таких потерь, однако для всех из них можно подобрать такие два изображения, что их мера отличия будет достаточно большой, но на глаз различия будут почти незаметными. И наоборот - можно подобрать изображения, сильно различающиеся на глаз, но имеющие небольшую меру отличия.
Введем сначала норму для значений атрибутов пикселей. Для полутоновых изображений, где на каждое значение атрибута пикселя отводится 8 бит:

Причем  , т.е. максимально возможное значение для такой нормы равно 255 x 255 = 65025. Для полноцветных изображений с тремя 8 -битными значениями атрибута пикселя (тремя 8 -битными каналами):
, т.е. максимально возможное значение для такой нормы равно 255 x 255 = 65025. Для полноцветных изображений с тремя 8 -битными значениями атрибута пикселя (тремя 8 -битными каналами):
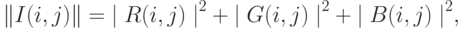
следовательно M* = 3 x 255 x 255 = 195075.
Стандартной мерой отличия является мера отношения сигнала к шуму ( PSNR - англ. Peak Signal-to-Noise Ratio), определяемая так:

где MSE(I1, I2) - другая мера - среднеквадратическая ошибка ( L2 -мера, MSE - англ. Mean Squared Error), определяемая так:

Тем не менее самой важной "мерой" оценки потерь является мнение наблюдателя. Чем меньше различий (а лучше - их отсутствие) обнаруживает наблюдатель, тем выше качество алгоритма сжатия.
Отметим важный факт, что алгоритмы сжатия с потерями часто предоставляют пользователю возможность выбирать объем "теряемых" данных. Таким образом, существует выбор между качеством и размером сжатого изображения. Естественно, что чем лучше визуальное качество при большем коэффициенте сжатия, тем алгоритм лучше.

