Параметрические кривые и их растеризация

В данном разделе рассматриваются основные виды параметрических кривых и алгоритмы их растеризации. Параметрические кривые, а также поверхности, применяются для описания более сложных, чем плоские, форм. Они находят широкое применение в графическом и промышленном дизайне.

В этом разделе будут рассматриваться вопросы построения кривых по контрольным точкам. Нас будут интересовать две задачи:

Интерполяция - построение кривой, проходящей через контрольные точки и обладающей некими дополнительными свойствами (часто гладкостью^{1Кривая n -й степени гладкости имеет непрерывную производную n -ого порядка; такой класс кривых обозначается как Cn .} );

Аппроксимация - приближение кривой (не обязательно проходит точно через данные точки, но удовлетворяет некоторому заданному свойству относительно этих точек).

В настоящее время большее применение находят аппроксимирующие кривые, поэтому в данном разделе им уделяется большее внимание.

4.1. Интерполяция сплайнами

Сплайн - кусочный многочлен степени K с непрерывной производной степени K - 1 в точках соединения сегментов.

Далее нас будут интересовать самые распространенные кубические сплайны.

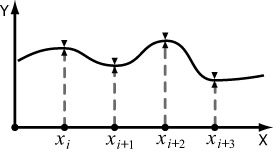
Понятие сплайна пришло из машиностроения, где сплайном называли гибкую линейку, закрепив которую в нужных местах, добивались плавной формы кривой, и затем чертили ее по этой линейке (см. рис. 4.1). Форма такой линейки, если ее рассматривать как функцию y(x), будет удовлетворять уравнению Эйлера-Бернулли:

где M(x) - момент изгиба вдоль линейки, E - модуль Юнга, зависящий от свойств материала рейки, I - момент инерции, определяемый формой кривой. Если мы фиксируем некоторые точки x_i подпорками, то момент изгиба на каждом отрезке меняется по линейному закону: M(x) = Ax + B. Подставляя M в исходное уравнение получаем

Дважды интегрируя, получаем уравнение кривой на данном отрезке:

y(x) = ax3 + bx2 + cx + d.

Рис. 4.1. Сплайн

Таким образом, форма физического сплайна описывается кусочным кубическим многочленом. Теперь рассмотрим задачу построения системы таких кубических многочленов для всего отрезка [x₀, x_N].

1. Для N отрезков имеем 4N коэффициентов: y(x) = a_ix³+b_ix²+c_ix + d_i для ;
2. Условия дают 2N уравнений;
3. Требование C¹ в точках дает N - 1 уравнений;
4. Требование C² в точках дает N - 1 уравнений.

Итого, имеем 4N - 2 уравнения; для того чтобы система была определенной, необходимы еще 2 уравнения. Их можно вывести, например, из заданных значений производных на границах или из условия периодичности. При корректно заданных условиях линейная относительно система имеет единственное решение. Подробнее см. в [8].