Параметрические кривые и их растеризация
Растеризация кривых Безье
Прямой метод
![\{x = x(t), y = y(t)\}, t \in [0, 1]](/sites/default/files/tex_cache/6af36043667a807fa65796a02f5d4370.png) (определяются по выражению (4.2)). Подберем шаг
(определяются по выражению (4.2)). Подберем шаг  так, чтобы
так, чтобы 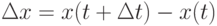 и
и ![\Delta y = y(t + \Delta t) - y(t) (t \in [0, 1])](/sites/default/files/tex_cache/bb4b202a099347d36a0323d09be3d32d.png) были меньше размера стороны пикселя d (если мы работаем в пиксельных координатах, то это 1 ), т. е. мы не пропустим ни одного пикселя при таких приращениях. Т.к.
были меньше размера стороны пикселя d (если мы работаем в пиксельных координатах, то это 1 ), т. е. мы не пропустим ни одного пикселя при таких приращениях. Т.к.  и
и 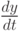 - многочлены, то, соответственно, легко найти максимумы их модулей Mx и My на отрезке [0, 1]. Положим M = max(Mx,My), тогда, взяв
- многочлены, то, соответственно, легко найти максимумы их модулей Mx и My на отрезке [0, 1]. Положим M = max(Mx,My), тогда, взяв  , получим что смещения по x и по y при каждом шаге не превосходят длины стороны пикселя.
, получим что смещения по x и по y при каждом шаге не превосходят длины стороны пикселя.
// x(t), y(t) заданы в пиксельных координатах => d = 1
// M - максимум модулей dx/dt и dy/dt на всем отрезке [0,1]
// round(x) - округляет x до ближайшего целого
dt = 1 / M;
t = 0;
while(t < 1)
{
x = x(t); // см. выражение 4.2
y = y(t); // см. выражение 4.2
plot( round(x) , round(y) );
t += dt;
}
Листинг
4.1.
Прямой метод растеризации кривой Безье
Недостаток данного алгоритма состоит в том, что при малых смещениях по x и y много итераций проходит зря, т.к. происходит повторная закраска одних и тех же пикселей.
Метод разбиения
Предложен де Кастелье. Рассмотрим пример этого алгоритма для кривой 4-го порядка с опорными точками P0P1P2P3 (см. рис. 4.6). Если рассмотреть участок между P0 и  , то он может быть задан как кривая Безье с опорными точками
, то он может быть задан как кривая Безье с опорными точками 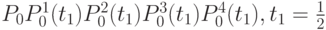 (почему это так, подробнее см., например, в [28]).
(почему это так, подробнее см., например, в [28]).
Аналогичные рассуждения справедливы и для участка между  и P4. Будем применять этот алгоритм рекурсивно для левой и правой частей, пока кривая не выродится в прямую с точностью до пикселя, а это так или иначе (все точки попадут в один пиксель) произойдет.
и P4. Будем применять этот алгоритм рекурсивно для левой и правой частей, пока кривая не выродится в прямую с точностью до пикселя, а это так или иначе (все точки попадут в один пиксель) произойдет.
plot(P) рисует пиксель с координатами, равными округленным до целых координатам точки P.
BBox(P1, . . . ,Pn) вычисляет наименьший ограничивающий прямоугольник для точек P1, . . . ,Pn.
// работаем в пиксельных координатах
// (размер пикселя равен 1x1)
// P0 - начальная точка кривой
// Pn - конечная точка кривой
DrawCurve(P0,P1, . . . ,Pn)
{
// Проверка на завершение
if( макс. длина ребра BBox(P0,P1, . . . , Pn) < 1 )
return;
if( P0,P1, . . . , Pn лежат на отрезке P0Pn
с точностью до пикселя )
{
Нарисовать отрезок P0Pn;
// (см. лекцию о растеризации отрезков)
return;
}
Найти P01,P02, . . . , P0{n-1} для t = 0,5;
// используя (4.1)
Найти P0n для t = 0,5; // используя (4.1)
Найти P1{n-1},P2{n-2}, . . . , P{n-1}1 для t = 0,5;
// используя (4.1)
plot(P0n);
// Нарисовать половинки (см. рис. 4.6)
DrawCurve( P0,P01, . . . , P0n);
DrawCurve( P0n,P1{n-1}, . . . , Pn);
}
Листинг
4.2.
Метод растеризации кривой Безье путем разбиения
Для построения кривых по большому множеству опорных точек пришлось бы использовать кривые Безье большого порядка, что привело бы к громоздким вычислениям; к тому же часто желательным является локальное влияние на форму кривой (для кривых Безье это не так). Поэтому чаще используют