Алгоритмические основы растровой графики
[+]
Московский государственный университет имени М.В.Ломоносова
Опубликован: 23.04.2007 | Доступ: свободный | Студентов: 3308 / 461 | Оценка: 4.18 / 3.71 | Длительность: 17:54:00
ISBN: 978-5-9556-0098-7
Тема: Компьютерная графика
Специальности: Программист
Теги: CIE, CMY, HSV, RAMDAC, ycbcr, YUV, алгоритмы, архитектуры, графика, квантование, компоненты, поиск, растеризация, САР, сжатие, сканеры, скользящее окно, форматы, цвета, электронная почта, элементы
Лекция 4:

Параметрические кривые и их растеризация
A
|
версия для печати
< Лекция 3 || Лекция 4: 12345 || Лекция 5 >

Сплайны, составленные из кривых Безье

Такие сплайны обладают свойством локальности влияния контрольных точек на форму кривой. Как и в случае интерполирующих сплайнов, будем искать сплайны определенной степени гладкости.

Для упрощения будем считать, что параметризация равномерная, т.е. длины отрезков, которые пробегает параметр на каждом из участков, равны. Для того чтобы рассмотреть условия на C1 и C2, необходимо найти производные кривых Безье:

P^N(t) =\sum\limits_{i=0}^{N}B_i ^N(t) \cdot P_i, \\ \frac{d}{dt}P^N(t) =N \cdot \sum\limits_{i=0}^{N-1}B_i ^{N-1}(t) \cdot (P_{i+1} - P_i), \\ \ldots \\ \frac{d^k}{dt^k}P^N(t) =\frac{N!}{(N - k)!} \cdot \sum\limits_{i=0}^{N-k}\Delta^k(P_i) B_i ^{N-k}(t) ,

где

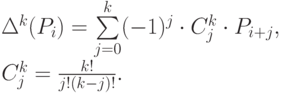
\Delta^k(P_i) = \sum\limits_{j=0}^{k}(-1)^j \cdot C_j ^k \cdot P_{i+j}, \\ C_j ^k =\frac{k!}{j!(k - j)!}.

Рассмотрим подробно случай кубических кривых Безье, которые являются самыми распространенными.

  1. Требование C1. Пусть заданы значения производных на концах ( d0 и d1 ), обозначим совпадающую последнюю контрольную точку предыдущей кривой и первую контрольную точку текущей как Pn:

    $ \frac{d}{dt}P^3(0) = 3(P_{n+1} - P_n) = d_0 \quad \Rightarrow \quad P_{n+1} = P_n + \frac{1}{3}d_0 \\ \frac{d}{dt}P^3(1) = 3(P_{n+3} - P_{n+2}) = d_1 \quad \Rightarrow \quad P_{n+2} = P_{n+3} - \frac{1}{3}d_1. $

    Таким образом, для того чтобы в точках стыковки производные были равны (d0 = d1), необходимо, чтобы

    P_{n-1} = P_n - (P_{n+1} - P_n ) \quad \Leftrightarrow \quad P_{n-1}- P_n = - (P_{n+1} - P_n )


    Рис. 4.7.
  2. Требование C2:

    $\frac{d}{dt}P^3(0) = 3(P_{n+1}- Pn) = 3d_1, \\ \frac{d}{dt}P^3(1) = 3(P_n - P_{n-1}) = 3d_2, \\ \frac{d^2}{dt^2}P^3(0) = 6(P_{n+2} - 2P_{n+1} + P_n), \\ = 6((P_{n+2} - P_{n+1}) + (P_n - P_{n+1})) = 6\Delta_1, \\ \frac{d^2}{dt^2}P^3(1) = 6(P_n - 2P_{n-1} + P_{n-2}), \\ = 6((P_n - P_{n-1}) + (P_{n-2} - P_{n-1})) = 6\Delta_2. $

    Из требования C1 в точках стыковки мы уже получили d =d_1 = d_2 \Leftrightarrow P_{n-1}P_n = P_nP_{n+1}. Далее, из требования C2 следует равенство \Delta = \Delta_1 = \Delta_2. Так как \Delta получаются сложением соответствующих векторов по правилу параллелограмма, то P_{n-2}P_{n+2} \quad \| \quad P_{n-1}P_{n+1} и, если обозначить точку пересечения Pn-2Pn-1 и Pn+2Pn+1 как Dn, то получим, что Pn-1Pn+1 - средняя линия треугольника Pn-2DnPn+2. Распространяя эти рассуждения на все точки стыковки, получаем, что для задания формы такого сплайна достаточно задать точки Dk, где k = 3i, i \in \overline{1,N/3}, где N + 1 - число опорных точек, и краевые точки - P0 и PN (см. рис. 4.9 ).

    Замечание. Для замкнутой кривой задание краевых точек не нужно.


    Рис. 4.8.

    Рис. 4.9.

Однако даже такие достаточно развитые средства аппроксимации кривыми Безье не позволяют построить окружность

\left\{ \begin{array}{c} x = \cos t \\ y = \sin t \\ \end{array} \right. ,
так как sin и cos для достаточно хорошего приближения требуют многочленов высокой степени. Поэтому вводится более широкий класс кривых, способ построения которых связан с представлением о проективном пространстве:

Дальше >>
< Лекция 3 || Лекция 4: 12345 || Лекция 5 >

Вопросы и ответы

вопросов: 0