Отсечение отрезков и многоугольников
5.1. Введение
На практике графические объекты всегда отображаются на конечном растре, границы которого соответствуют границам экрана или внеэкранного буфера. Растеризация на конечном растре требует возможности отсечения растеризуемого объекта относительно границ растра, т.е. удаления частей растеризуемого объекта, лежащих за пределами растра. Выполнение алгоритма растеризации без предварительного отсечения приведет к ошибке при попытке осуществить изменение цвета пикселя с координатами за пределами растра (это может привести к изменению цвета не того пикселя или даже к системному сбою).
Можно было бы просто проверять, лежит ли пиксель внутри растра непосредственно перед изменением его цвета. К сожалению, такое решение в большинстве случаев слишком неэффективно. Во-первых, подобная проверка сама по себе чрезвычайно замедлит растеризацию. Во-вторых, в тех случаях, когда значительная часть объекта лежит вне растра, растеризация для этой области будет выполняться вхолостую и отсечение подобных областей опять-таки ускорит вычисления.
В этом разделе мы рассмотрим алгоритмы отсечения отрезка и многоугольника относительно границ прямоугольника (иногда мы будем называть этот прямоугольник "окном").
5.2. Отсечение отрезков
Алгоритм Сазерлэнда-Коэна
Алгоритм Сазерлэнда-Коэна осуществляет отсечение отрезка относительно прямоугольника со сторонами, параллельными координатным осям.
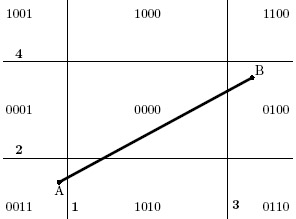
Пронумеруем стороны прямоугольника так, как это показано на рис. 5.1, и классифицируем все точки в зависимости от их положения по отношению к отсекающим прямым 1, 2, 3, 4. Для этого сопоставим каждой области, на которые разбивают плоскость прямые, 4 -битный код.
Установим эти биты следующим образом:
| 0 бит | если точка лежит левее прямой 1 ( x < xлево ) |
| 1 бит | если точка лежит ниже прямой 2 ( y < yниз ) |
| 2 бит | если точка лежит правее прямой 3 ( x > xправо ) |
| 3 бит | если точка лежит выше прямой 4 ( y > yверх ) |
Тогда для отрезка AB на рис. 5.1 будем иметь: код точки A = 0011, код точки B = 0100.
Пусть A - код точки-начала отрезка, B - код точки-конца отрезка. Рассмотрим три возможных случая.
- A = B = 0000. Этот случай означает, что обе точки лежат внутри прямоугольника (т. е. отсечение не требуется).
-
 . В этом случае точки лежат по одну сторону от какой-либо отсекающей линии (с внешней ее стороны). Следовательно, отрезок полностью лежит вне окна.
. В этом случае точки лежат по одну сторону от какой-либо отсекающей линии (с внешней ее стороны). Следовательно, отрезок полностью лежит вне окна. - Если не выполнены условия 1 или 2, то необходимо находить точки пересечения с некоторыми из отсекающих прямых (для прямых, которые пересекает AB, соответствующий бит в A xor B установлен в 1 ). Для этого разобьем отрезок найденными точками пересечения и затем применим тот же анализ кодов концов для полученных подотрезков.
Один из возможных вариантов реализации окончательного алгоритма приведен ниже:
// (xлево, yниз, xправо, yверх) - отсекающий прямоугольник;
// Функция код(<точка>) возвращает битовый код,
// значение которого описано выше;
Отсечь( отрезок AB )
{
while(( код(A) | код(B) ) AND (!( код(A) & код(B) )))
{
if( код(A) == 0) // т.е. A внутри
// меняем координаты местами,
// чтобы A всегда лежала снаружи
поменять(A,B);
if( код(A) & 1 ) // т.е. A лежит слева
{
A.x += (B.y - A.y)*(xлево-A.x)/(B.x - A.x);
A.y = xлево;
}
else if( код(A) & 2 ) // т.е. A лежит сверху
{
A.x += (B.x - A.x)*(yверх-A.y)/(B.y - A.y);
A.y = yверх;
}
else if( код(A) & 4 ) // т.е. A лежит справа
{
A.y += (B.y - A.y)*(xправо-A.x)/(B.x - A.x);
A.x = xправо;
}
else if( код(A) & 8 ) // т.е. A лежит снизу
{
A.x += (B.x - A.x)*(yниз -A.y)/(B.y - A.y);
A.y = yниз;
}
}
return AB; // Вернуть отсеченный отрезок
}
Листинг
5.1.
Алгоритм Сазерлэнда-Коэна
Алгоритм Сазерлэнда-Коэна может быть обобщен на случай отсечения отрезка параллелепипедом в трехмерном пространстве. В этом случае код, конечно, уже будет длины 6 (по числу отсекающих граней).
Алгоритм средней точки
Алгоритм решает ту же задачу: отсечение отрезка относительно прямоугольника. Случаи, в которых отрезок лежит целиком снаружи или внутри окна, выявим методом, изложенным в алгоритме Сазерлэнда-Коэна.
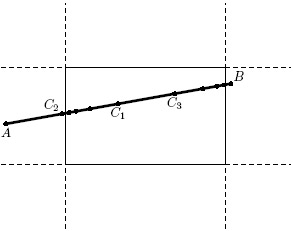
В общем случае возьмем среднюю точку нашего отрезка AB (обозначим ее C1 ) и применим к отрезкам AC1 и C1B этот алгоритм рекурсивно. Следующие средние точки отрезков AC1 и C1B обозначим C2 и C3 соответственно, см. рис. 5.2. И так далее, пока размер оставшихся отрезков не станет меньше размера пикселя.
В примере на рис. 5.2 после второй итерации отрезок AC2 будет отсечен, и для него дальнейшее половинное деление производиться не будет; C1C3 лежит целиком внутри области отсечения, он будет нарисован, и для него дальнейшее половинное деление также производиться не будет. Остальные части будем делить дальше.
Отсечь( отрезок AB )
{
if( длина AB меньше размера пикселя ) return;
if( AB лежит вне отсекающего прямоугольника ) return;
if( AB лежит внутри отсекающего прямоугольника )
{
Отобразить AB;
return;
}
Отсечь (A, (A+B)/2);
Отсечь ((A+B)/2),B);
}
Листинг
5.2.
Алгоритм средней точки
Алгоритм средней точки прост, но не очень эффективен на практике, так как требует большой глубины рекурсии. В большинстве случаев алгоритм Сазерлэнда-Коэна предпочтительнее. Прием с делением отрезка пополам может оказаться эффективным при отсечении относительно сложной непрямоугольной области, для которой проверить принадлежность точки к окну существенно проще, чем найти пересечение отрезка с границей.
Алгоритм средней точки также обобщается на случай трехмерного пространства тривиальным образом.