Отсечение отрезков и многоугольников
5.3. Отсечение многоугольников
Рассмотрим теперь задачу отсечения многоугольника относительно прямоугольника и алгоритм Сазерлэнда-Ходжмана [48], позволяющий проводить такое отсечение.
Ключевым моментом в этом алгоритме является сведение задачи отсечения прямоугольником к задаче отсечения полуплоскостями. Действительно, прямоугольник представляется в виде пересечения четырех полуплоскостей (по сути, этим же представлением мы пользовались и в алгоритме Сазерлэнда-Коэна). Поэтому достаточно поочередно отсечь части многоугольника, лежащие вне каждой полуплоскости.
Пусть многоугольник задан своими вершинами: P1P2 . . . PN. 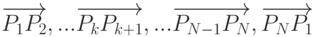 - направленные ребра этого многоугольника.
- направленные ребра этого многоугольника.
Относительно произвольной полуплоскости  каждое направленное ребро
каждое направленное ребро  может находиться в следующих положениях:
может находиться в следующих положениях:
- целиком внутри полуплоскости:
 ,
,  ;
; - целиком вне полуплоскости:
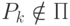 ,
, 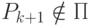 ;
; - выходить из полуплоскости:
 ,
, 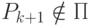 ;
; - входить в полуплоскость:
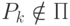 ,
,  .
.
Следующий алгоритм выводит в качестве результата вершины отсеченного многоугольника, обходя исходные вершины.
Отсечь P[1]...P[N] относительно полуплоскости
{
//L - граница полуплоскости
for( i = 1; i <= N; i++ )
{
j = i+1;
if( j == N+1 )
j = 1;
if( P[i]P[j] пересекает L )
{
I = пересечение( P[i]P[j], L );
вывести(I);
}
if( P[j]видима )
вывести(P[j]);
}
}
Листинг
5.5.
Алгоритм Сазерлэнда-Ходжмана
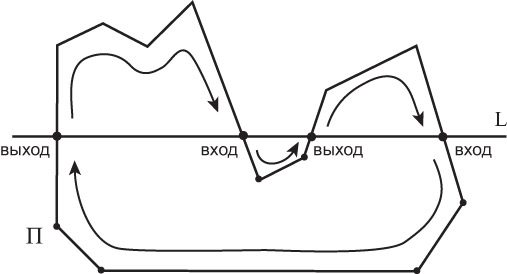
Данный алгоритм выводит вершины отсеченного многоугольника в порядке обхода. Пример работы алгоритма Сазерлэнда-Ходжмана приведен на рис. 5.5.
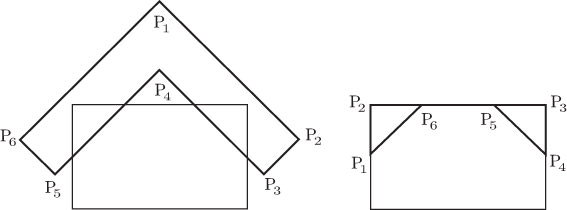
После проведения отсечения четырьмя полуплоскостями получается многоугольник, отсеченный относительно прямоугольника. Заметим, что данный алгоритм очевидным образом применим для отсечения любого выпуклого многоугольного окна - достаточно представить это окно в виде пересечений полуплоскостей.
Практически единственным недостатком алгоритма Сазерлэнда-Ходжмана является не совсем корректная обработка случаев, когда результатом отсечения являются несколько изолированных многоугольников. Результат алгоритма Сазерлэнда-Ходжмана в этом случае содержит многоугольники и связывающие их отрезки (рис. 5.6).