Отсечение отрезков и многоугольников

Алгоритм Цируса-Бека

Алгоритм Цируса-Бека [25] отсекает отрезок P₁P₂, используя его параметрическое представление:

( 5.1)

Данный алгоритм применим не только в случае отсечения прямоугольником со сторонами, параллельными осям координат, но и в случае, если отсекаемая область ограничена любым выпуклым многоугольником.

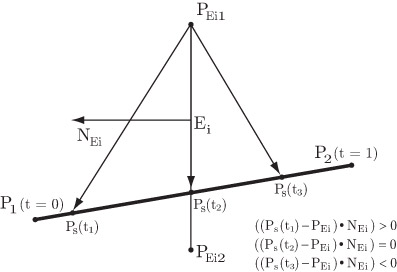
Рассмотрим отдельно ребро E_i отсекающего многоугольника. Нормаль к нему ориентируем во внешнюю сторону отсекающего многоугольника, для этого удобно считать, что точки отсекающего контура обходятся против часовой стрелки; тогда если ребро - это , то нормаль N_Ei будет пропорциональна (y_Ei2-y_Ei1, x_Ei1- x_Ei2), см. рис. 5.3.

Тогда область, отсекаемая прямой, на которой лежит ребро (обозначим ее L_i ), соответствует точкам P, для которых^{1Здесь и далее (x, y) - скалярное произведение векторов x и y.} (P-P_Ei),N_Ei) > 0, где P_Ei - любая точка на ребре E_i. Точка пересечения прямой, на которой лежит отрезок с отсекающей прямой L_i, находится из уравнения

((Ps(t) - PEi),NEi) = 0.

Разрешая его, получаем, что

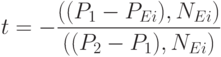( 5.2)

в том случае, если 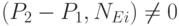. Если же ((P₂ - P₁),N_Ei) = 0 это означает, что отсекаемый отрезок параллелен L_i и не существует единственной точки их пересечения. Такие случаи алгоритм игнорирует.

Рис. 5.3. Пересечение отрезка с ребром.

Для алгоритма Цируса-Бека также важно в каком направлении (внутрь отсекающего многоугольника или из него) проходит точка при движении по отрезку от P₁ к P₂, т.е. при изменении t от 0 до 1. Это определяется знаком ((P₂ - P₁),N_Ei). Будем обозначать такие точки пересечения как:

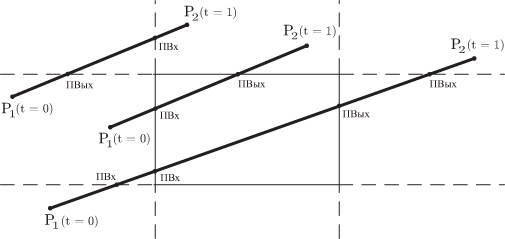
После того как рассчитаны координаты t для всех возможных пересечений с прямыми L_i, следует выбрать максимальную координату из потенциально входящих пересечений t_ВхMax и минимальную из потенциально выходящих t_ВыхMin. Если прямая, на которой лежит отрезок P₁P₂, пересекает отсекающий многоугольник, то t_ВхMax < t_ВыхMin. В этом случае, если пересечение непусто, то P_s(t₁)P_s(t₂) будет искомым отсеченным отрезком. В противном случае отрезок полностью лежит вне отсекаемой области.

Рис. 5.4. Возможные случаи пересечений в алгоритме Цируса-Бека.

Вычислить NEi и взять PEi = PEi1 для каждого ребра.

Отсечь(отрезок P1P2)
{
   if(P1 == P2)
      отсечь как точку;
   else
     {
          D = P2 - P1;
          t_Вх = 0;
          t_Вых = 1;

          foreach( ребро Ei из отсекающего многоугольника )
          {
              dp = (D,NEi);
              if( dp != 0 ) // случай dp == 0 игнорируется
              {

if( dp < 0 )
             {
                 if( t > t_Вх )
                 t_Вх = t;
              }
                   else // dp > 0
                   {
                        if( t < t_Вых )
                        t_Вых = t;
                          }
                  }
        }

          if( t_Вх < t_Вых )
              return отрезок Ps(t_Вх)Ps(t_Вых);
          else
             return '
      }
}

Алгоритм Цируса-Бека также может быть обобщен до случая отсечения отрезка произвольным выпуклым многогранником в трехмерном пространстве.