Московский государственный университет имени М.В.Ломоносова
Опубликован: 23.04.2007 | Доступ: свободный | Студентов: 3344 / 480 | Оценка: 4.18 / 3.71 | Длительность: 17:54:00
ISBN: 978-5-9556-0098-7
Тема: Компьютерная графика
Специальности: Программист
Лекция 5:
Отсечение отрезков и многоугольников
Алгоритм Лианга-Барского
Алгоритм Лианга-Барского [39] является более эффективным вариантом алгоритма Цируса-Бека в случае, если отсекающий многоугольник - это прямоугольник со сторонами, параллельными осям координат. В этом случае вычисление промежуточных величин упрощается ( P1 = (x1, y1),P2 = (x2, y2) ):
| Ребро | NEi | PEi | ((P2 - P1),NEi) | t |
|---|---|---|---|---|
| левое: x = xлево |
(-1, 0) | (xлево, yверх) | x1 - x2 | 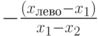 |
| нижнее: y = yниз |
(0,-1) | (xлево, yниз) | y1 - y2 |  |
| правое: x = xправо |
(1, 0) | (xправо, yниз) | x2 - x1 | 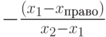 |
| верхнее: y = yверх |
(0, 1) | (xправо, yверх) | y2 - y1 | 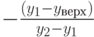 |
// (xлево, yниз, xправо, yверх) - отсекающий прямоугольник;
Отсечь(отрезок P1P2)
{
dx = P2.x - P1.x;
dy = P2.y - P1.y;
if( dx == 0 AND dy == 0 )
отсечь как точку;
else
{
t_Вх = 0;
t_Вых = 1;
// Отсечь_t может модифицировать t_Вх и t_Вых
// (& означает передачу по адресу)
if( Отсечь_t( dx, xлево - P1.x, &t_Вх, &t_Вых ) )
if( Отсечь_t( -dx, P1.x - xправо, &t_Вх, &t_Вых ) )
if( Отсечь_t( dy, yниз - P1.y, &t_Вх, &t_Вых ) )
if( Отсечь_t( -dy, P1.y - yверх, &t_Вх, &t_Вых ) )
{
if( t_Вх > 0 )
{
P1.x = P1.x + dx*t_Вх;
P1.y = P1.y + dy*t_Вх;
}
if( t_Вых < 1 )
{
P2.x = P1.x + dx*t_Вых;
P2.y = P1.y + dy*t_Вых;
}
return отрезок P1P2;
}
return '
}
}
// Проверить пересечение с ребром
// denom, num - 'знаменатель' и 'числитель' выражения (5.2)
// t_Вх и t_Вых передаются по адресу (обозначено *),
// они могут быть модифицированы;
// возвращает логическую переменную:
// true - продолжать отcечение
// false - закончить отcечение,
// отрезок полностью вне прямоугольника
bool Отсечь_t( denom, num, *t_Вх, *t_Вых )
{
if( denom > 0 ) // Потенциально входящее пересечение
{
t = num / denom;
if( t > t_Вых )
// t_ВхMax > t_ВыхMin: отрезок полностью снаружи
return false;
else if( t > t_Вх ) // Модифицируем t_Вх
t_Вх = t;
}
else if( denom < 0 ) // Потенциально выходящее пересечение
{
t = num / denom;
if( t < t_Вх )
// t_ВхMax > t_ВыхMin: отрезок полностью снаружи
return false;
else if( t < t_Вых ) // Модифицируем t_Вых
t_Вых = t;
}
else if( num > 0 )
// отрезок параллелен ребру и полностью снаружи
return false;
return true;
}
Листинг
5.4.
Алгоритм Лианга-Барского
Эксперименты, проведенные авторами на случайных наборах данных [39], показали, что их алгоритм на 25-62% быстрее алгоритма Сазерлэнда-Коэна. Поэтому в настоящее время алгоритм Лианга-Барского получил большее распространение.
