Алгоритмические основы растровой графики
[+]
Московский государственный университет имени М.В.Ломоносова
Опубликован: 23.04.2007 | Доступ: свободный | Студентов: 3280 / 442 | Оценка: 4.18 / 3.71 | Длительность: 17:54:00
ISBN: 978-5-9556-0098-7
Тема: Компьютерная графика
Специальности: Программист
Теги: CIE, CMY, HSV, RAMDAC, ycbcr, YUV, алгоритмы, архитектуры, графика, квантование, компоненты, поиск, растеризация, САР, сжатие, сканеры, скользящее окно, форматы, цвета, электронная почта, элементы
Лекция 4:

Параметрические кривые и их растеризация
A
|
версия для печати
< Лекция 3 || Лекция 4: 12345 || Лекция 5 >

Сплайны, составленные из рациональных кривых Безье

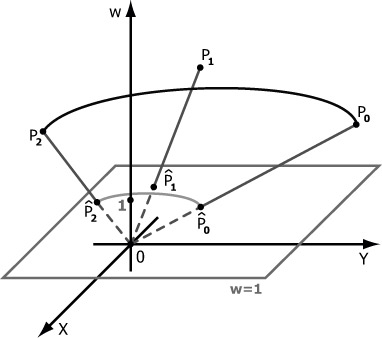
Пусть у нас есть пространственная кривая Безье P0P1 . . . PN в системе координат OXY w. Спроецируем все точки исходной кривой на плоскость w = 1, т.е.:

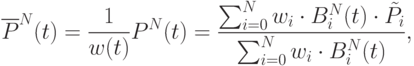
\overline{P}^N(t) =\frac{1}{w(t)}P^N(t) = \frac{\sum_{i=0}^{N}w_i \cdot B_i^N(t) \cdot \tilde{P}_i}{\sum_{i=0}^{N}w_i \cdot B_i^N(t)},

где

P_i = \left[ \begin{array}{c} w_i \cdot \tilde{P}_i \\ w_i \end{array} \right] = \left( \begin{array}{c} w_ix_i \\ w_iy_i \\ w_i \end{array} \right) \mbox{ (см. рис. 4.10.)}

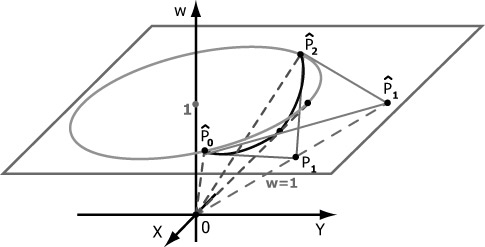
Полученная кривая, лежащая в плоскости w = 1, и называется рациональной двумерной кривой Безье. Аналогичным образом можно получать рациональные кривые Безье и в пространстве большего числа измерений.

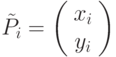
\tilde{P}_i = \left( \begin{array}{c} x_i \\ y_i \end{array} \right)
будем называть опорными точками рациональной кривой Безье, а wi - весовыми функциями.

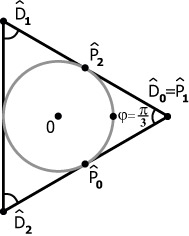
Рассмотрим пример представления окружности, составленной из 3-х рациональных кубических кривых Безье. Возьмем для примера один из сегментов (см. рис. 4.11). Положим 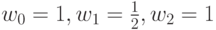w_0 = 1, w_1 = \frac{1}{2} , w_2 = 1, а

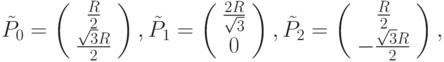
$\tilde{P}_0 = \left( \begin{array}{c} \frac{R}{2} \\ \frac{\sqrt{3}R}{2} \end{array} \right), \tilde{P}_1 = \left( \begin{array}{c} \frac{2R}{\sqrt{3}} \\ 0 \end{array} \right), \tilde{P}_2 = \left( \begin{array}{c} \frac{R}{2} \\ -\frac{\sqrt{3}R}{2} \end{array} \right), $

где R - радиус окружности.

Итоговое изображение представлено на рис. 4.12.

Рациональная кривая Безье.

Рис. 4.10. Рациональная кривая Безье.

Растеризовать такие кривые можно теми же двумя способами, что и для обыкновенных кривых Безье. При этом в алгоритме рекурсивного разбиения разбивается исходная кривая в проективном пространстве.

B-сплайны

B-сплайны являются обобщением кривых Безье. Они также представимы в линейной комбинации контрольных точек. Пусть заданы порядок кривой n, потенциальное количество участков m, вектор узлов

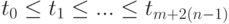
t_0 \le t_1 \le . . . \le t_{m+2(n-1)}

и контрольные точки 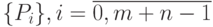\{P_i\} , i = \overline{0,m + n - 1}. Если ti = ti+1 = . . . = ti+l и соответственно Pi = Pi+1 = . . . = Pi+l, то говорят об узле ti кратности l. Как правило, для кривой порядка n в начале и в конце ставятся узлы кратности n, так как при этом концы кривой будут совпадать с крайними контрольными точками.

Сегмент окружности, представленный рациональной кривой Безье.

Рис. 4.11. Сегмент окружности, представленный рациональной кривой Безье.
Изображение окружности.

Рис. 4.12. Изображение окружности.

Формулы Кокса - де Бура (Cox - de Boor) рекурсивно определяют B-сплайн:

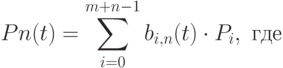Pn(t) = \sum\limits_{i=0}^{m+n-1}b_{i,n}(t) \cdot P_i, \mbox{ где} ( 4.3)
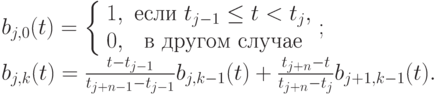
b_{j,0}(t) = { \left\{ \begin{array}{cc} 1, & \text{если } t_{j-1} \le t < t_j, \\ 0, & \text{в другом случае} \\ \end{array} \right. }; \\ b_{j,k}(t) = \frac{t-t_{j-1}}{t_{j+n-1}-t_{j-1}}b_{j,k-1}(t) + \frac{t_{j+n}- t}{t_{j+n}-t_j}b_{j+1,k-1}(t).

Если узлы кратные, то в (4.3) возникают неопределенности вида \frac{0}{0}, которые по определению должны разрешаться как 0. Многочисленные полезные свойства этих кривых находятся за рамками данной книги. Подробную информацию можно найти в [28], [8].

Кратко остановимся только на вопросе растеризации данных кривых. Можно выделить три основных подхода.

  • Последовательное вычисление значений по параметрам. Этот метод аналогичен по сути прямому методу растеризации кривых Безье (см. алг. 4.2). Производится либо напрямую по формулам (4.4), либо по алгоритму де Бура, который является аналогом алгоритма де Кастелье для B-сплайнов.

    Алгоритм де Бура

    Для t \in [t_I , t_{I+1}), I \in \overline{n - 1,m+ n - 1}

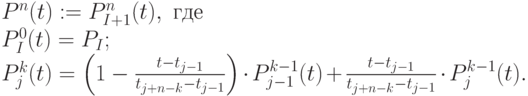
    P^n(t) := P_{I+1}^n(t), \mbox{ где} \\ P_I^0(t) = P_I ; \\ P_j^k(t) = \left(1 - \frac{t-t_{j-1}}{t_{j+n-k}-t_{j-1}}\right) \cdot P_{j-1}^{k-1}(t) + \frac{t-t_{j-1}}{t_{j+n-k}-t_{j-1}} \cdot P_j^{k-1}(t). ( 4.4)

    Если узлы кратные, то в (4.4) также могут возникнуть неопределенности вида \frac{0}{0}, которые по определению должны разрешаться как 0.

  • Рекурсивное разбиение до определенного порога с помощью алгоритма Осло. Алгоритм Осло [22] позволяет добавлять сразу много промежуточных контрольных точек в существующий B-сплайн, до тех пор пока точность приближения не станет достаточной для растеризации (расстояние между соседними точками не будет превышать размеров пикселя).
  • Преобразование B-сплайна на каждом отрезке в отдельную кривую Безье и растеризация уже этой кривой методами, изложенными выше. Найти контрольные точки кривой Безье для каждого отрезка [ti, ti+1] можно при помощи вставки узлов ti до тех пор пока их кратность не достигнет n. Новые контрольные точки B-сплайна, которые также будут контрольными точками для кривых Безье на каждом отрезке [ti, ti+1], будут получены в результате стандартной процедуры добавления узлов в B-сплайн (см. например, [28]).

Самыми распространенными в геометрическом моделировании в настоящее время являются Неоднородные рациональные B-сплайны (англ. NURBS). Неоднородность означает, что промежутки между соседними узлами ti могут быть различными. Рациональные они в том же смысле, что и рациональные кривые Безье ( "Параметрические кривые и их растеризация" ), т.е. проекция B-сплайна из проективного пространства. Это наиболее широкий из рассмотренных классов кривых.

4.3. Заключение

Специфика данного курса не предполагает детального изучения математических свойств рассмотренных выше кривых; особенно это касается лишь кратко рассмотренных B-сплайнов. Всех интересующихся описанием этих вопросов, а также тех, кто хотел бы узнать более подробно о вышеизложенном материале, отсылаем к книгам [8], [28].

Также за рамками данной лекции остались кривые разбиения. О них можно узнать подробнее из [47].

Дальше >>
< Лекция 3 || Лекция 4: 12345 || Лекция 5 >

Вопросы и ответы

вопросов: 0