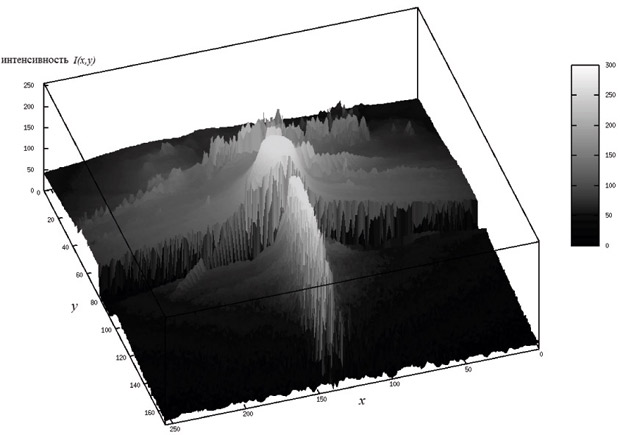
Сжатие изображений с потерями
14.3. Изображение как функция
Будем рассматривать изображение как функцию двух переменных, определенную в точках конечного растра (имеется в виду точечная модель растра, см. определение "Основные понятия. Представление цвета в машинной графике" ). I(x, y) - значение атрибута пикселя (например номер в палитре, интенсивность), зависящее от цветовой модели представления изображения (см. рис. 14.1 и рис. 14.2). Множество таких функций на точках фиксированного конечного растра образуют конечномерное евклидово пространство RX,Y размерности m x n (|X|=m,|Y|= n) со скалярным произведением
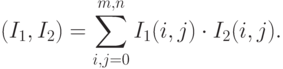
Будем отождествлять с таким пространством L2(X x Y ). В таком пространстве существует базис (см. [3]), т.е. такая система элементов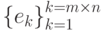 
из RX,Y и такой набор не равных одновременно нулю коэффициентов 
, что для любой функции I из этого пространства выполнено
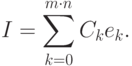
Если дополнительно предположить ортонормальность базиса, т.е.
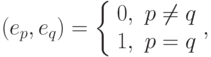
то выполняется следующее соотношение:
Ck = (I, ek).
Дискретное Преобразование Фурье
Напомним определение двумерного дискретного преобразования Фурье функции I:
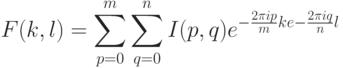
для всех k = 1 . . .m, l = 1 . . . n. Обратное преобразование определяется так:
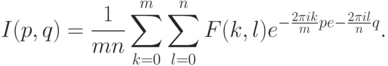
Система функций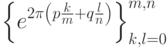 
образует базис в пространстве функций-изображений (см. [3]).
Такое преобразование очень популярно в области обработки изображений, однако в общем виде практически не используется для сжатия изображений из-за плохой частотно-пространственной локализации.
Дискретное косинусное преобразование
Рассмотрим определение дискретного косинусного преобразования (ДКП) [43]. Пусть изображение имеет размеры N x N. Прямое преобразование записывается так:
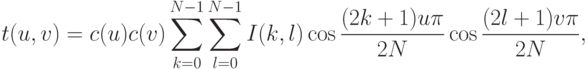
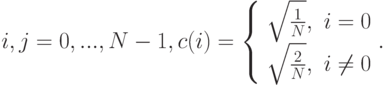
Обратное преобразование имеет следующий вид:
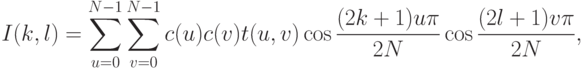
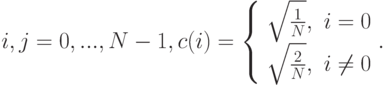
Дискретное преобразование обладает свойствами.
- Некоррелированность коэффициентов. Коэффициенты независимы друг от друга, т.е. точность представления одного коэффициента не зависит от любого другого.
- "Уплотнение" энергии (англ. energy compaction). Преобразование сохраняет основную информацию в малом количестве коэффициентов. Данное свойство сильнее всего проявляется на фотореалистичных изображениях.
Коэффициенты t(u, v) - это амплитуды пространственных частот изображения. В случае изображений с плавными переходами большая часть информации содержится в низкочастотном спектре ( "Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений" ).
Отметим, что применение дискретного косинус-преобразования эквивалентно применению дискретного преобразования Фурье примерно двойной длины к действительным (некомплексным) и четно симметричным данным (эквивалентность вытекает из того, что преобразование Фурье четной действительной функции четно и действительно).