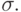Фильтрация изображений
Сглаживающие фильтры
Сглаживающие фильтры действуют на изображение аналогично мутному стеклу из примера в начале лекции: изображение становится нерезким, размытым. Простейший прямоугольный сглаживающий фильтр радиуса r задается при помощи матрицы размера (2r + 1) x (2r + 1), все значения которой равны
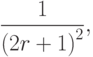
Рассмотрим особенности сглаживания при помощи прямоугольного фильтра. Характерной чертой этого фильтра, отличающей его, к примеру, от эффекта расфокусировки линз в реальной жизни, является то, что образом белой точки на черном фоне будет равномерно серый квадрат. Проявления этого эффекта хорошо заметны и на нижнем правом изображении рис. 8.1: длинные узкие объекты "размазываются" в прямоугольники равномерной интенсивности.

Рис. 8.1. Прямоугольный сглаживающий фильтр. Слева вверху - пример изображения, справа вверху - результат фильтрации для r = 1, слева внизу - результат фильтрации для r = 3,справа внизу - результат фильтрации для r = 5.
Для чего могут применяться сглаживающие фильтры? Одним из их возможных применений является шумоподавление, т.е. задача восстановления исходного изображения, к пикселям которого добавлен случайный шум. Шум меняется независимо от пикселя к пикселю и, при условии, что математическое ожидание значения шума равно нулю, шумы соседних пикселей будут компенсировать друг друга. Чем больше окно фильтрации, тем меньше будет усредненная интенсивность шума, однако при этом будет происходить и существенное размытие значащих деталей изображения.
Естественным предположением об исходном незашумленном изображении будет схожесть значений интенсивности пикселей, находящихся рядом. Причем чем меньше расстояние между пикселями, тем больше вероятность их похожести. Это и отличает исходное незашумленное изображение от шумовой компоненты, для которой схожесть пикселей никак не зависит от расстояния между ними. Исходя из вышесказанного можно предположить, что шумоподавление при помощи прямоугольного фильтра имеет существенный недостаток: пиксели на расстоянии r от обрабатываемого оказывают на результат тот же эффект, что и соседние.
Более эффективное шумоподавление можно, таким образом, осуществить, если влияние пикселей друг на друга будет уменьшаться с расстоянием. Этим свойством обладает гауссовский фильтр с ядром:
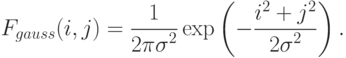 |
( 8.3) |
Гауссовский фильтр имеет ненулевое ядро бесконечного размера. Однако ядро фильтра очень быстро убывает к нулю при удалении от точки (0, 0), и потому на практике можно ограничиться сверткой с окном небольшого размера вокруг (0, 0) (например, взяв радиус окна равным 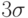 ).
).
Гауссовская фильтрация также является сглаживающей. Однако, в отличие от прямоугольного фильтра, образом точки при гауссовой фильтрации будет симметричное размытое пятно, с убыванием яркости от середины к краям, что гораздо ближе к реальному размытию от расфокусированных линз. Как и следовало ожидать, гауссовская фильтрация более эффективна при шумоподавлении (рис. 8.2): влияние пикселей друг на друга при гауссовой фильтрации обратно пропорционально квадрату расстояния между ними. Как видно из (8.3), коэффициент пропорциональности, а следовательно, и степень размытия, определяются параметром